
已知函数f(x)=Asin(2x+θ),其中A≠0,θ∈(0, ).
).
(1)若函数f(x)的图象过点E(- ,1),F(
,1),F( ,
, ),求函数f(x)的解析式;
),求函数f(x)的解析式;
(2)如图,点M,N是函数y=f(x)的图象在y轴两侧与x轴的两个相邻交点,函数图象上一点P(t, )满足
)满足 ·
· =
= ,求函数f(x)的最大值.
,求函数f(x)的最大值.
科目:高中数学 来源: 题型:解答题
将形如 的符号称二阶行列式,现规定
的符号称二阶行列式,现规定 , 函数
, 函数 =
= 在一个周期内的图象如图所示,
在一个周期内的图象如图所示, 为图象的最高点,
为图象的最高点,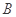 、
、 为图象与
为图象与 轴的交点,且
轴的交点,且 为正三角形。
为正三角形。
(1)求 的值及函数
的值及函数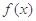 的单调递增区间;
的单调递增区间;
(2)若 ,在
,在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,两个圆形飞轮通过皮带传动,大飞轮O1的半径为2r(r为常数),小飞轮O2的半径为r,O1O2=4r.在大飞轮的边缘上有两个点A,B,满足∠BO1A=,在小飞轮的边缘上有点C.设大飞轮逆时针旋转,传动开始时,点B,C在水平直线O1O2上.
(1)求点A到达最高点时A,C间的距离;
(2)求点B,C在传动过程中高度差的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,单位圆(半径为1的圆)的圆心O为坐标原点,单位圆与y轴的正半轴交于点A,与钝角α的终边OB交于点B(xB,yB),设∠BAO=β.
(1)用β表示α;
(2)如果 sin β=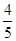 ,求点B(xB,yB)坐标;
,求点B(xB,yB)坐标;
(3)求xB-yB的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某广告公司设计一个凸八边形的商标,它的中间是一个正方形,外面是四个腰长为 ,顶角为
,顶角为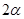 的等腰三角形.
的等腰三角形.
(1)若角 时,求该八边形的面积;
时,求该八边形的面积;
(2)写出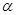 的取值范围,当
的取值范围,当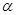 取何值时该八边形的面积最大,并求出最大面积.
取何值时该八边形的面积最大,并求出最大面积.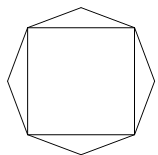
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com