
分析 根据指数函数的单调性求出命题p为真命题时a的范围,利用二次方程的实根分布求出命题q为真命题时a的范围;据复合命题的真假与构成其简单命题真假的关系将“p或q为真,p且q为假”转化为p q的真假,列出不等式解得.
解答 解:若p真,则f(x)=(2a-6)x在R上单调递减,
∴0<2a-6<1,
∴3<a<$\frac{7}{2}$.
若q真,令f(x)=x2-3ax+2a2+1,则应满足:
$\left\{\begin{array}{l}{△{=(-3a)}^{2}-4({2a}^{2}+1)≥0}\\{-\frac{-3a}{2}>3}\\{f(3)=9-9a+{2a}^{2}+1>0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a≥2或a≤-2}\\{a>2}\\{a<2或a>\frac{5}{2}}\end{array}\right.$,
∴a>$\frac{5}{2}$,
又由题意应有p真q假或p假q真.
①若p真q假,则 $\left\{\begin{array}{l}{3<a<\frac{7}{2}}\\{a≤\frac{5}{2}}\end{array}\right.$,a无解.
②若p假q真,则 $\left\{\begin{array}{l}{a≤3或a≥\frac{7}{2}}\\{a>\frac{5}{2}}\end{array}\right.$,
∴由2a-6>0且2a-6≠1,可得a>$\frac{7}{2}$.
点评 本题考查复合命题的真假与简单命题真假的关系;考查二次方程实根分布.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | [0,π] | B. | $[0,\frac{π}{2})∪[\frac{3π}{4},π)$ | C. | $[0,\frac{π}{2})∪[\frac{π}{2},π)$ | D. | $[0,\frac{π}{2}]∪[\frac{3π}{4},π)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,-\frac{40}{3}+2ln3]∪(-1,1)∪(1,+∞)$ | B. | $(-∞,-\frac{34}{3}+2ln3]∪(1,+∞)$ | ||
| C. | $(-∞,-\frac{34}{3}+2ln3]∪[-1,1)∪(1,+∞)$ | D. | $(-∞,-\frac{40}{3}+2ln3]∪(1,+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<-e | B. | a>1 | C. | a>e | D. | a<-3或a>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
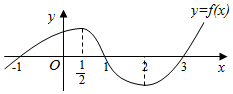
| A. | $(-∞,\frac{1}{2})∪(\frac{1}{2},2)$ | B. | (-1,0)∪(1,3) | C. | $(-∞,\frac{1}{2})∪(\frac{1}{2},+∞)$ | D. | $(-∞,\frac{1}{2})∪(2,+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ②④ | C. | ①④ | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com