
【题目】下列说法正确的是( )
A.![]() ,“
,“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
B.“![]() 为真命题”是“
为真命题”是“![]() 为真命题”的必要不充分条件
为真命题”的必要不充分条件
C.命题“![]()
![]() ”的否定是:“
”的否定是:“![]() 使得
使得![]() ”
”
D.命题p:“![]()
![]() ”,则
”,则![]() 是真命题
是真命题
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中,平面PBC⊥平面ABC,∠ACB=90°,BC=PC=2,若AC=PB,则三棱锥P﹣ABC体积的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
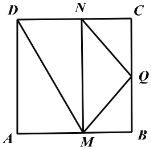
【题目】如图,在边长等于2正方形![]() 中,点Q是
中,点Q是![]() 中点,点M,N分别在线段
中点,点M,N分别在线段![]() 上移动(M不与A,B重合,N不与C,D重合),且
上移动(M不与A,B重合,N不与C,D重合),且![]() ,沿着
,沿着![]() 将四边形
将四边形![]() 折起,使得二面角
折起,使得二面角![]() 为直二面角,则三棱锥
为直二面角,则三棱锥![]() 体积的最大值为________;当三棱锥
体积的最大值为________;当三棱锥![]() 体积最大时,其外接球的表面积为________.
体积最大时,其外接球的表面积为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
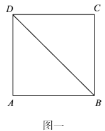
【题目】如图一所示,四边形![]() 是边长为
是边长为![]() 的正方形,沿
的正方形,沿![]() 将
将![]() 点翻折到
点翻折到![]() 点位置(如图二所示),使得二面角
点位置(如图二所示),使得二面角![]() 成直二面角.
成直二面角.![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
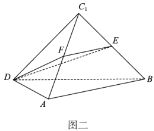
(1)求证:![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是公差为1的等差数列,
是公差为1的等差数列,![]() 是单调递增的等比数列,且
是单调递增的等比数列,且![]() ,
,![]() ,
,![]() .
.
(1)求![]() 和
和![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和
项和![]() ,求
,求![]() ;
;
(3)若数列![]() 的前
的前![]() 项积为
项积为![]() ,求
,求![]() .
.
(4)数列![]() 满足
满足![]() ,
,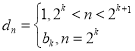 ,其中
,其中![]() ,
,![]() ,求
,求![]() .
.
(5)解决数列问题时,经常需要先研究陌生的通项公式,只有先把通项公式研究明白,然后尽可能转化为我们熟悉的数列问题,由此使问题得到解决.通过对上面(2)(3)(4)问题的解决,你认为研究陌生数列的通项问题有哪些常用方法,要求介绍两个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,以
,以![]() 为折痕把
为折痕把![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且
的位置,且![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 的中点,二面角
的中点,二面角![]() 等于60°,求直线
等于60°,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为直线
为直线![]() 的倾斜角),以坐标原点
的倾斜角),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的直角坐标方程,并求
的直角坐标方程,并求![]() 时直线
时直线![]() 的普通方程;
的普通方程;
(2)若直线![]() 和曲线
和曲线![]() 交于两点
交于两点![]() ,点
,点![]() 的直角坐标为
的直角坐标为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com