
是否存在圆锥曲线C,同时满足下列两个条件:
(1)原点O及直线![]() 为曲线C的焦点和相应的准线;
为曲线C的焦点和相应的准线;
(2)被直线![]() 垂直平分的直线截曲线C所得的弦长恰好为
垂直平分的直线截曲线C所得的弦长恰好为![]() 。
。
若存在,求出曲线C的方程,若不存在,说明理由。
解:设存在符合题设的圆锥曲线C,此曲线离心率为![]() (
(![]() >0),P(x,y)是曲线C上任一点。
>0),P(x,y)是曲线C上任一点。
由圆锥曲线的定义有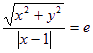
化简整理得,![]() ①
①
设曲线C被直线![]() 垂直平分,其弦长为
垂直平分,其弦长为![]() 的弦所在直线方程为
的弦所在直线方程为![]() ,这弦的两个端点
,这弦的两个端点![]()
将![]() 代入①式中,消去y得
代入①式中,消去y得
![]() ②
②
由题意![]() 0,
0,
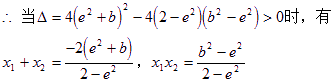
由此可解得AB的中点D的坐标为
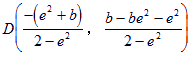
由条件(2),中点D在![]() ,于是有:
,于是有:
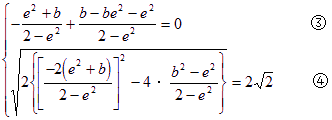
解③![]() ,代入④得
,代入④得![]() 。
。
经检验符合题意,因此符合条件的曲线C存在,其方程为![]() 。
。
这是一道开放性的题目,探求满足上述两个条件的圆锥曲线是否存在,本题的难点是题目没有具体的给出圆锥曲线的形状,由条件(1)给出焦点和相应的准线,因此可考虑用圆锥曲线统一定义,设离心率为![]() ,通过计算,推理,探求
,通过计算,推理,探求![]() 的存在性。
的存在性。


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•广州三模)如图,长为m+1(m>0)的线段AB的两个端点A和B分别在x轴和y轴上滑动,点M是线段AB上一点,且
(2013•广州三模)如图,长为m+1(m>0)的线段AB的两个端点A和B分别在x轴和y轴上滑动,点M是线段AB上一点,且| AM |
| MB |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:高三数学教学与测试 题型:044
是否存在一条圆锥曲线C,同时满足下列两个条件:(1)以点F(-1,0)为焦点,以直线x=-4为准线;(2)与抛物线 =x-2有且只有一个公共点.若存在,求出曲线C的方程;若不存在,说明理由.
=x-2有且只有一个公共点.若存在,求出曲线C的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
设A是单位圆x2+y2=1上任意一点,l是过点A与x轴垂直的直线,D是直线l与x轴的交点,点M在直线l上,且满足![]() 当点A在圆上运动时,记点M的轨迹为曲线C。
当点A在圆上运动时,记点M的轨迹为曲线C。
(1)求曲线C的方程,判断曲线C为何种圆锥曲线,并求其焦点坐标。
(2)过原点斜率为K的直线交曲线C于P,Q两点,其中P在第一象限,且它在y轴上的射影为点N,直线QN交曲线C于另一点H,是否存在m,使得对任意的K>0,都有PQ⊥PH?若存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com