
【题目】已知点![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() 是椭圆的焦点,直线
是椭圆的焦点,直线![]() 的斜率为
的斜率为![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,当
两点,当![]() 的面积最大时,求直线
的面积最大时,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)设出F,由直线AF的斜率为![]() ,求得c,结合离心率求得a,再由隐含条件求得b,则椭圆方程可求;
,求得c,结合离心率求得a,再由隐含条件求得b,则椭圆方程可求;
(2)当l⊥x轴时,不合题意;当直线l斜率存在时,设直线l:y=kx-2,联立直线方程和椭圆方程,由判别式大于0求得k的范围,再由弦长公式求得|PQ|,由点到直线的距离公式求得O到l的距离,代入三角形面积公式,化简后换元,利用基本不等式求得最值,进一步求出k值,则直线方程可求.
试题解析:
(1)设![]() ,解得
,解得![]() ,又
,又![]() ,
, ![]() 椭圆
椭圆![]() .
.
(2)当![]() 轴时,不合题意;当直线
轴时,不合题意;当直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() ,联立
,联立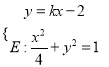 ,得
,得![]() ,由
,由![]() ,得
,得![]() ,即
,即![]() 或
或![]() ,
, ![]() ,从而
,从而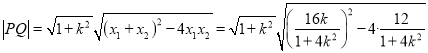
![]() ,又点
,又点![]() 到直线
到直线![]() 的距离
的距离![]() 的面积
的面积![]() ,设
,设![]() ,则
,则![]() ,
,
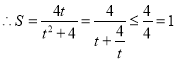 ,当且仅当
,当且仅当![]() ,即
,即![]() 时,等号成立,且
时,等号成立,且![]() ,此时
,此时![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,直线
,直线![]() 是函数
是函数![]() 图象的一条对称轴.
图象的一条对称轴.
(1)求![]() 的值,并求
的值,并求![]() 的解析式;
的解析式;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有且只有一个实数解,求实数
上有且只有一个实数解,求实数![]() 的取值范围;
的取值范围;
(3)已知函数![]() 的图象是由
的图象是由![]() 图象上的所有点的横坐标伸长到原来的2倍,然后再向左平移
图象上的所有点的横坐标伸长到原来的2倍,然后再向左平移![]() 个单位得到,若
个单位得到,若![]() ,
, ![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为评估新教改对教学的影响,挑选了水平相当的两个平行班进行对比试验,甲班采用创新教法,乙班仍采用传统教法,一段时间后进行水平测试,成绩结果全部落在![]() 区间内(满分100分),并绘制频率分布直方图如图所示,两个班人数均为60人,成绩80分及以上为优良.
区间内(满分100分),并绘制频率分布直方图如图所示,两个班人数均为60人,成绩80分及以上为优良.
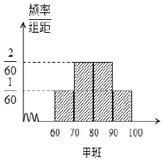
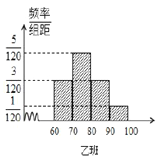
(1)根据以上信息填好![]() 联表,并判断出有多大的把握认为学生成绩优良与班级有关?
联表,并判断出有多大的把握认为学生成绩优良与班级有关?
(2)以班级分层抽样,抽取成绩优良的5人参加座谈,现从5人中随机选3人来作书面发言,求发言人至少有2人来自甲班的概率.
(以下临界值及公式仅供参考)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
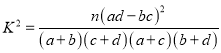 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某直三棱柱(侧棱与底面垂直的三棱柱)被削去上底后的直观图与三视图中的侧视图、俯视图,在直观图中, ![]() 是
是![]() 的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
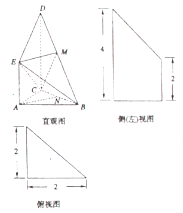
(1)求出该几何体的体积;
(2)若![]() 是
是![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程是
的参数方程是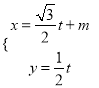 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com