
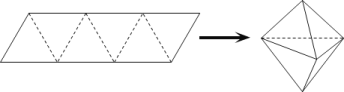
【题目】农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,古称“角黍”,平行四边形形状的纸片是由六个边长为![]() 的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为______;若该六面体内有一球,则该球表面积的最大值为______.
的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为______;若该六面体内有一球,则该球表面积的最大值为______.
【答案】![]()
![]()
【解析】
该六面体看成由两个全等的正四面体组合而成,正四面体的棱长为![]() ,在棱长为
,在棱长为![]() 的正四面体
的正四面体![]() 中,其高为顶点
中,其高为顶点![]() 和底面
和底面![]() 中心的连线段,易求;则该正四面体的体积易求,该六面体的体积可求. 当该六面体内有一球,且该球体积取最大值时,该球与
中心的连线段,易求;则该正四面体的体积易求,该六面体的体积可求. 当该六面体内有一球,且该球体积取最大值时,该球与![]() 相切,过球心作
相切,过球心作![]() ,则
,则![]() 就是球半径,利用等面积法可求半径
就是球半径,利用等面积法可求半径![]() ,则球的表面积可求.
,则球的表面积可求.
解:该六面体看成由两个全等的正四面体组合而成,正四面体的棱长为![]() ,如图,
,如图,
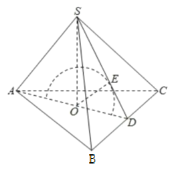
在棱长为![]() 的正四面体
的正四面体![]() 中,取
中,取![]() 中点为
中点为![]() ,连接
,连接![]() ,
,![]() ,
,
作![]() 平面
平面![]() ,垂足
,垂足![]() 在
在![]() 上,
上,
则 ,
,![]() ,
,![]() ,
,
则该正四面体的体积为![]() ,
,
该六面体的体积![]() .
.
当该六面体内有一球,且该球体积取最大值时,球心为![]() ,
,
且该球与![]() 相切,过球心作
相切,过球心作![]() ,则
,则![]() 就是球半径,
就是球半径,
因为![]() ,所以球半径
,所以球半径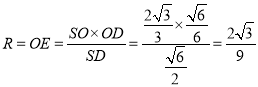 ,
,
所以该球表面积的最大值为: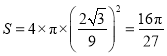 .
.
故答案为:![]() ;
;![]() .
.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:高中数学 来源: 题型:
【题目】已知函数f (x)=lnx,g(x)=ex.
(1)若函数φ (x) = f (x)-![]() ,求函数φ (x)的单调增区间;
,求函数φ (x)的单调增区间;
(2)设直线l为函数的图象上一点A(x0,f (x0))处的切线.证明:在区间(1,+∞)上存在唯一的x0,使得直线l与曲线y=g(x)相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
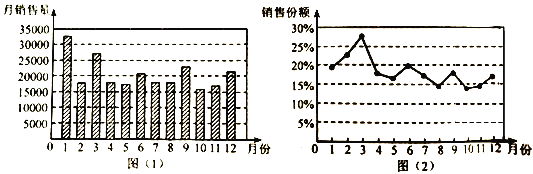
【题目】图(![]() )是某品牌汽车
)是某品牌汽车![]() 年月销量统计图,图(
年月销量统计图,图(![]() )是该品牌汽车月销量占所属汽车公司当月总销量的份额统计图,则下列说法错误的是( )
)是该品牌汽车月销量占所属汽车公司当月总销量的份额统计图,则下列说法错误的是( )
A.该品牌汽车![]() 年全年销量中,
年全年销量中,![]() 月份月销量最多
月份月销量最多
B.该品牌汽车![]() 年上半年的销售淡季是
年上半年的销售淡季是![]() 月份,下半年的销售淡季是
月份,下半年的销售淡季是![]() 月份
月份
C.![]() 年该品牌汽车所属公司
年该品牌汽车所属公司![]() 月份的汽车销量比
月份的汽车销量比![]() 月份多
月份多
D.该品牌汽车![]() 年下半年月销量相对于上半年,波动性小,变化较平稳
年下半年月销量相对于上半年,波动性小,变化较平稳
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com