练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在中，角A,B,C所对的边分别是a,b,c,且.

    （1）证明：；

    （2）若，求.

    【答案】（1）证明见解析；（2）4.

    【解析】（1）根据正弦定理，可设===k(k>0)．

    则a=ksin A，b=ksin B，c=ksin C．

    代入+=中，有+=，

    变形可得sin Asin B=sin Acos B+cos Asin B=sin(A+B)．

    在中，由A+B+C=π，得sin(A+B)=sin(π–C)=sin C，

    所以sin Asin B=sin C．

    （2）由已知，b2+c2–a2=bc，根据余弦定理，有

    cos A==．

    所以sin A==．

    由（1），sin Asin B=sin Acos B+cos Asin B，

    所以sin B=cos B+sin B，

    故tan B==4．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= ax2﹣（2a+1）x+2lnx（a∈R）
    （1）当a= 时，求函数f（x）的单调区间；
    （2）设g（x）=（x2﹣2x）ex ， 如果对任意x1∈（0，2]，均存在x2∈（0，2]，使得f（x1）＜g（x2）成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列函数中，既是奇函数又是增函数的是（ ）
    A.y=x+1
    B.y=﹣x3
    C.y=x|x|
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）对一切实数x，y都有f（x+y）﹣f（y）=x（x+2y+1）成立，且f（1）=0．
    （1）求f（0）的值；
    （2）求f（x）的解析式；
    （3）若g（x）=kx﹣2k+5，对任意的m∈[1，4]，总存在n∈[1，4]，使得f（m）=g（n）成立，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

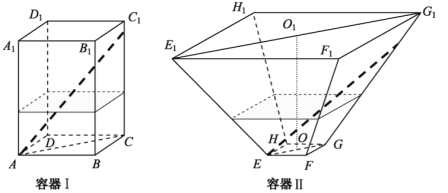
    【题目】如图，水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm，容器Ⅰ的底面对角线AC的长为10cm，容器Ⅱ的两底面对角线，的长分别为14cm和62cm．分别在容器Ⅰ和容器Ⅱ中注入水，水深均为12cm．现有一根玻璃棒l，其长度为40cm．（容器厚度、玻璃棒粗细均忽略不计）

    （1）将放在容器Ⅰ中，的一端置于点A处，另一端置于侧棱上，求没入水中部分的长度；

    （2）将放在容器Ⅱ中，的一端置于点E处，另一端置于侧棱上，求没入水中部分的长度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知双曲线C： （a＞0，b＞0）过点A（1，0），且离心率为
    （1）求双曲线C的方程；
    （2）已知直线x﹣y+m=0与双曲线C交于不同的两点A，B，且线段AB的中点在圆x2+y2=5上，求m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，O为等腰三角形ABC内一点，⊙O与△ABC的底边BC交于M，N两点，与底边上的高AD交于点G，且与AB，AC分别相切于E，F两点．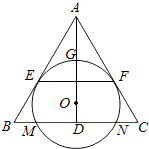

    （1）证明：EF∥BC；
    （2）若AG等于⊙O的半径，且AE=MN=2 ，求四边形EBCF的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列幂函数在（﹣∞，0）上为减函数的是 （ ）
    A.
    B.
    C.y=x3
    D.y=x2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯（ ）

    A. 1盏 B. 3盏 C. 5盏 D. 9盏

    查看答案和解析>>

    同步练习册答案