
【题目】设函数![]() .
.
(1)若函数![]() 在
在![]() 上为减函数,求实数
上为减函数,求实数![]() 的最小值;
的最小值;
(2)若存在![]() ,使
,使![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)最小值为![]() ;(II)
;(II)![]()
【解析】试题分析: ![]() 在
在![]() 上为减函数,等价于
上为减函数,等价于![]() 在
在![]() 上恒成立,进而转化为
上恒成立,进而转化为![]() ,根据二次函数的性质可得
,根据二次函数的性质可得![]()
![]() 命题“若存在
命题“若存在![]() ,
,![]()
![]() ,使
,使![]() 成立”等价于
成立”等价于
“当![]() 时,有
时,有 ![]() ”, 由
”, 由![]() 易求
易求![]() ,从而问题等价于“当
,从而问题等价于“当![]() 时,有
时,有![]() ”,分
”,分![]()
![]() ,
,![]()
![]() 两种情况讨论:
两种情况讨论:
当![]() 是易求
是易求![]() ,当
,当![]() 时可求得
时可求得![]() 的值域为
的值域为![]() ,再按
,再按![]()
![]() 两种情况讨论即可
两种情况讨论即可
解析:(1)由已知得![]() ,
, ![]()
因![]() 在
在![]() 上为减函数,故
上为减函数,故![]() 在
在![]() 上恒成立。
上恒成立。
所以当![]() 时
时![]() 。
。
又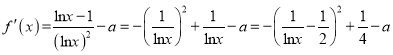 ,
,
故当![]() 时,即
时,即![]() 时,
时, ![]() .
.
所以![]() ,于是
,于是![]() ,故
,故![]() 的最小值为
的最小值为![]() .
.
(2)命题“若存在![]() ,
,![]()
![]() ,使
,使![]() 成立”等价于
成立”等价于
“当![]() 时,”
时,” ![]() ”,
”,
由(1),当![]() 时,
时, ![]() ,
, ![]()
![]() .
.
问题等价于:“当![]() 时,有
时,有![]() ”.
”.
当![]() ,由(1),
,由(1),![]() 在
在![]() 为减函数,
为减函数,
则![]() ,故
,故![]() .
.
当![]() 时,由于
时,由于![]() 在
在![]() 上的值域为
上的值域为![]()
(i)![]() ,即
,即![]() ,
, ![]() 在
在![]() 恒成立,故
恒成立,故![]() 在
在![]() 上为增函数,
上为增函数,
于是, ![]() ,矛盾。
,矛盾。
(ii)![]() ,即
,即![]() ,由
,由![]() 的单调性和值域知,
的单调性和值域知,
存在唯一![]() ,使
,使![]() ,且满足:
,且满足:
当![]() 时,
时, ![]() ,
, ![]() 为减函数;当
为减函数;当![]() 时,
时, ![]() ,
, ![]() 为增函数;
为增函数;
所以, ![]() ,
, ![]()
所以, ![]() ,与
,与![]() 矛盾。
矛盾。
综上得![]()


科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() 且
且![]() )是定义域为R的奇函数.
)是定义域为R的奇函数.
(Ⅰ)求t的值;
(Ⅱ)若函数![]() 的图象过点
的图象过点![]() ,是否存在正数m
,是否存在正数m![]() ,使函数
,使函数![]() 在
在![]() 上的最大值为0,若存在,求出m的值;若不存在,请说明理由.
上的最大值为0,若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确命题的个数是( )
(1)cosα≠0是 ![]() 的充分必要条件
的充分必要条件
(2)f(x)=|sinx|+|cosx|,则f(x)最小正周期是π
(3)若将一组样本数据中的每个数据都加上同一个常数后,则样本的方差不变
(4)设随机变量ζ服从正态分布N(0,1),若P(ζ>1)=p,则 ![]() .
.
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)= ![]() ,直线y=m与函数f(x)的图象相交于四个不同的点,从小到大,交点横坐标依次记为a,b,c,d,有以下四个结论 ①m∈[3,4)
,直线y=m与函数f(x)的图象相交于四个不同的点,从小到大,交点横坐标依次记为a,b,c,d,有以下四个结论 ①m∈[3,4)
②abcd∈[0,e4)
③a+b+c+d∈ ![]()
④若关于x的方程f(x)+x=m恰有三个不同实根,则m取值唯一.
则其中正确的结论是( )
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一条直线与一个平面垂直,则称此直线与平面构成一个“正交线面对”.那么在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是( )
A. 48 B. 36 C. 24 D. 18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com