
【题目】某农科所为改良玉米品种,对已选出的一组玉米的茎高进行统计,获得茎叶图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
抗倒伏 | 易倒伏 | 总计 | |
矮茎 | |||
高茎 | |||
总计 |
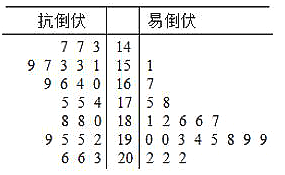
(1)请完成以上![]() 列联表,并判断是否可以在犯错误的概率不超过0.01的前提下,认为抗倒伏与玉米矮茎有关?
列联表,并判断是否可以在犯错误的概率不超过0.01的前提下,认为抗倒伏与玉米矮茎有关?
(2)为改良玉米品种,现采用分层抽样的方法从抗倒伏的玉米中抽出5株,再从这5株玉米中选取2株进行杂交试验,则选取的植株均为矮茎的概率是多少?
参考公式: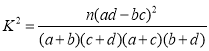 (其中
(其中![]() )
)
参考数据:
| 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【答案】(1)答案见解析.(2)![]()
【解析】
(1)根据统计数据填写出![]() 的列联表,利用公式求得
的列联表,利用公式求得![]() 的值,对照临界值,即可得到结论;
的值,对照临界值,即可得到结论;
(2)利用列举法求出基本事件的总数,利用古典概型的概率计算公式,即可求解.
(1)根据统计数据得![]() 列联表如下:
列联表如下:
抗倒伏 | 易倒伏 | 总计 | |
矮茎 | 15 | 4 | 19 |
高茎 | 10 | 16 | 26 |
总计 | 25 | 20 | 45 |
由于![]() 的观测值
的观测值![]() ,
,
因此可以在犯错误的概率不超过0.01的前提下,认为抗倒伏与玉米矮茎有关.
(2)根据题意得,抽到的高茎玉米有2株,设为A,B,抽到的矮茎玉米有3株,设为a,b,c,
从这5株玉米中取出2株的取法有AB,Aa,Ab,Ac,Ba,Bb,Bc,ab,ac,bc,共10种,其中均为矮茎的选取方法有ab,ac,bc,共3种,
因此,选取的植株均为矮茎的概率是![]()


科目:高中数学 来源: 题型:
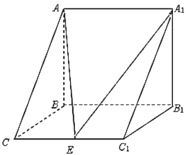
【题目】如图,三棱柱![]() 中,
中,![]() 侧面
侧面![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,点
,点![]() 是棱
是棱![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,ABCD为平行四边形,![]() 平面PAB,
平面PAB,![]() ,
,![]() .M为PB的中点.
.M为PB的中点.
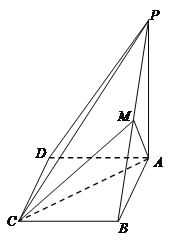
(1)求证:PD//平面AMC;
(2)求锐二面角B-AC-M的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,(
,( ![]() 为参数),
为参数),![]() 为曲线
为曲线![]() 上的动点,动点
上的动点,动点![]() 满足
满足![]() (
(![]() 且
且![]() ),
),![]() 点的轨迹为曲线
点的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程,并说明
的方程,并说明![]() 是什么曲线;
是什么曲线;
(2)在以坐标原点为极点,以![]() 轴的正半轴为极轴的极坐标系中,
轴的正半轴为极轴的极坐标系中, ![]() 点的极坐标为
点的极坐标为![]() ,射线
,射线![]() 与
与![]() 的异于极点的交点为
的异于极点的交点为![]() ,已知
,已知![]() 面积的最大值为
面积的最大值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com