练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，点A，B分别是椭圆 的长轴的左右端点，点F为椭圆的右焦点，直线PF的方程为： 且PA⊥PF．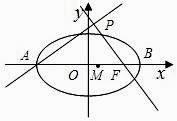
    （1）求直线AP的方程；
    （2）设点M是椭圆长轴AB上一点，点M到直线AP的距离等于|MB|，求椭圆上的点到点M的距离d的最小值．

    【答案】
    （1）解：由题意得 ，A的坐标为（﹣6，0）

    则直线AP的方程为： ．


    （2）解：设M（m，0），则 ，解得m=2或m=18（舍去），故M（2，0）．

    ，x∈[﹣6，6]，

    所以当 时，dmin2=15，即


    【解析】（1）根据两直线垂直，求得AP的斜率，利用椭圆方程求得A的坐标，然后利用点斜式求得直线AP的方程．（2）设出点M的坐标，利用两点间的距离公式利用题设建立等式求得m，进而可利用两点间的距离公式，表示出椭圆上的点到点M的距离d，利用x的范围和二次函数的单调性求得函数的最小值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知全集U=R，A={x| ≤2x≤8}，B={x|x＞0}，C={x|m＜x＜m+2}
    （Ⅰ）求A∩（UB）；
    （Ⅱ）若A∩C=，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设Sn为等差数列{an}的前n项的和a1=1， ，则数列 的前2017项和为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，正方体AC1的棱长为1，过点A作平面A1BD的垂线，垂足为点H，则以下命题中，错误的命题是（ ）
    A.点H是△A1BD的垂心
    B.AH垂直平面CB1D1
    C.AH的延长线经过点C1
    D.直线AH和BB1所成角为45°

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】假设某种设备使用的年限x（年）与所支出的维修费用y（元）有以下统计资料：

    使用年限x

    2

    3

    4

    5

    6

    维修费用y

    2.2

    3.8

    5.5

    6.5

    7.0

    参考数据： ， ，
    如果由资料知y对x呈线性相关关系．试求：
    （1） ；
    （2）线性回归方程 =bx+a．
    （3）估计使用10年时，维修费用是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知全集U=R，集合A={x∈R|2x﹣3≥0}，B={x|1＜x＜2}，C={x∈N|1≤x＜a}．
    （Ⅰ）求A∪B；
    （Ⅱ）若C中恰有五个元素，求整数a的值；
    （Ⅲ）若A∩C=，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

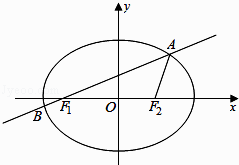
    【题目】如图，已知椭圆 的离心率为 ，F1、F2为其左、右焦点，过F1的直线l交椭圆于A、B两点，△F1AF2的周长为 ．
    （1）求椭圆的标准方程；
    （2）求△AOB面积的最大值（O为坐标原点）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知命题p：“1≤x≤5是x2﹣（a+1）x+a≤0的充分不必要条件”，命题q：“满足AC=6，BC=a，∠CAB=30°的△ABC有两个”．若￢p∧q是真命题，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C的圆心在x轴上，点 在圆C上，圆心到直线2x﹣y=0的距离为 ，则圆C的方程为（ ）
    A.（x﹣2）2+y2=3
    B.（x+2）2+y2=9
    C.（x±2）2+y2=3
    D.（x±2）2+y2=9

    查看答案和解析>>

    同步练习册答案