
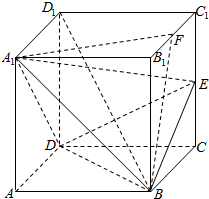
 已知正方体ABCD-A1B1C1D1的棱长为2a,E为CC1的中点,F为B1C1的中点.
已知正方体ABCD-A1B1C1D1的棱长为2a,E为CC1的中点,F为B1C1的中点.分析 (1)连AC,A1C1,根据正方体的几何特征,可得AA1⊥BD,AC⊥BD,由线面垂直的判定定理,可得BD⊥平面ACC1A1,再根据线面垂直的性质,即可得到BD⊥A1E.
(2)设AC∩BD=O,则O为BD的中点,连A1O,EO,结合(1)的结论,可得∠A1EO即为二面角A1-BD-E的平面角,解三角形A1EO,可以求出为二面角A1-BD-E为直二面角,即平面A1BD⊥平面EBD;
(3)与(2)同法,即可证明结论.
解答 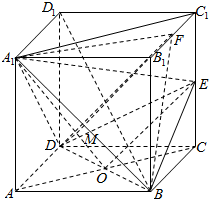 证明:(1)连AC,A1C1.∵正方体AC1中,AA1⊥平面ABCD,∴AA1⊥BD.
证明:(1)连AC,A1C1.∵正方体AC1中,AA1⊥平面ABCD,∴AA1⊥BD.
∵正方形ABCD,AC⊥BD且AC∩AA1=A.∴BD⊥平面ACC1A1 且E∈CC1.∴A1E?平面ACC1A1.∴BD⊥A1E.
(2)设AC∩BD=O,则O为BD的中点,连A1O,EO.
由(1)得BD⊥平面A1ACC1,∴BD⊥A1O,BD⊥EO.
∴∠A1OE即为二面角A1-BD-E的平面角.
∵AB=a,E为CC1中点,∴A1O=$\sqrt{6}$a,EO=$\sqrt{3}$a,A1E=3a.
∴A1O2+OE2=A1E2.∴A1O⊥OE.∴∠A1OE=90°.
∴平面A1BD⊥平面BDE.
(3)取A1B的中点M,连接DM,F1M,则∠F1MD即为二面角F-A1B-D的平面角.
∴DM=$\sqrt{6}$a,F1M=$\sqrt{3}$a,DF=3a,
∴F1M2+DM2=DF2.∴DM⊥FM.∴∠F1MD=90°.
∴平面A1BF⊥平面A1BD.
点评 本题考查的知识点是线面垂直的性质,平面与平面垂直的判定.熟练掌握空间线线、线面及面面之间位置关系的转化是关键.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:选择题
| A. | y=x2 | B. | $y={x^{\frac{1}{3}}}$ | C. | y=x-1 | D. | $y={x^{-\frac{1}{2}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com