
【题目】已知直线x+y﹣1=0与椭圆 ![]() 相交于A,B两点,线段AB中点M在直线
相交于A,B两点,线段AB中点M在直线 ![]() 上.
上.
(1)求椭圆的离心率;
(2)若椭圆右焦点关于直线l的对称点在单位圆x2+y2=1上,求椭圆的方程.
【答案】
(1)解:设A,B两点的坐标分别为(x1,y1),(x2,y2),
由 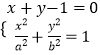 得:(a2+b2)x2﹣2a2x+a2﹣a2b2=0.
得:(a2+b2)x2﹣2a2x+a2﹣a2b2=0.
△=﹣(2a2)2﹣(a2+b2)(a2﹣a2b2)>0,即a2+b2>1.
x1+x2= ![]() ,y1+y2=﹣( x1+x2)+2=
,y1+y2=﹣( x1+x2)+2= ![]() ,
,
∴点M的坐标为( ![]() ,
, ![]() ).
).
又点M在直线l上,
∴ ![]() ﹣
﹣ ![]() =0,
=0,
∴a2=2b2=2(a2﹣c2),∴a2=2c2,
∴ ![]()
(2)解:由(1)知b=c,设椭圆的右焦点F(b,0)关于直线 ![]() 的对称点为(x0,y0),
的对称点为(x0,y0),
由 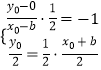 ,解得
,解得 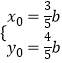
∵x02+y02=1,
∴ ![]() ,
,
∴b2=1,显然有a2+b2=3>1.
∴所求的椭圆的方程为 ![]()
【解析】(1)设出A、B两点的坐标,联立直线与椭圆的方程得关于x的一元二次方程;由根与系数的关系,可得x1+x2 , y1+y2;从而得线段AB的中点坐标,代入直线l的方程,得出a、c的关系,从而求得椭圆的离心率.(2)设椭圆的右焦点坐标为F(b,0),F关于直线l的对称点为(x0 , y0),则由互为对称点的连线被对称轴垂直平分,可得方程组,解得x0、y0;代入圆的方程 x02+y02=1,得出b的值,从而得椭圆的方程.
【考点精析】关于本题考查的椭圆的标准方程,需要了解椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能得出正确答案.
才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】设函数y=f(x)的定义域为D,值域为A,如果存在函数x=g(t),使得函数y=f[g(t)]的值域仍是A,那么称x=g(t)是函数y=f(x)的一个等值域变换.
(1)判断下列函数x=g(t)是不是函数y=f(x)的一个等值域变换?说明你的理由; ① ![]() ;
;
②f(x)=x2﹣x+1,x∈R,x=g(t)=2t , t∈R.
(2)设f(x)=log2x的定义域为x∈[2,8],已知 ![]() 是y=f(x)的一个等值域变换,且函数y=f[g(t)]的定义域为R,求实数m、n的值.
是y=f(x)的一个等值域变换,且函数y=f[g(t)]的定义域为R,求实数m、n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取100件样本,测量这些样本的一项质量指标值,由测量结果得如下频数分布表:
质量指标 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125] |
频数 | 6 | 26 | 38 | 22 | 8 |
则样本的该项质量指标值落在[105,125]上的频率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱 ![]() 中,底面
中,底面 ![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 分别为线段
分别为线段 ![]() ,
, ![]() 的中点.
的中点.
(1)求证: ![]() ||平面
||平面 ![]() ;
;
(2)四棱柱 ![]() 的外接球的表面积为
的外接球的表面积为 ![]() ,求异面直线
,求异面直线 ![]() 与
与 ![]() 所成的角的大小.
所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD的底面是正方形,SA⊥底面ABCD,E是SC上一点. 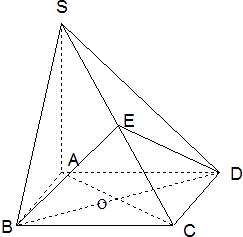
(1)求证:平面EBD⊥平面SAC;
(2)设SA=4,AB=2,求点A到平面SBD的距离;
(3)设SA=4,AB=2,当OE丄SC时,求二面角E﹣BD﹣C余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若f(x)是定义在(0,+∞)上的函数,当x>1时,f(x)>0,且满足 ![]() .
.
(1)求f(1)的值;
(2)判断并证明函数的单调性;
(3)若f(2)=1,解不等式 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com