
【题目】已知椭圆C的方程为![]() ,离心率为
,离心率为![]() ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线![]() 的焦点.
的焦点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过动点![]() 的直线交
的直线交![]() 轴的负半轴于点
轴的负半轴于点![]() ,交C于点
,交C于点![]() (
(![]() 在第一象限),且
在第一象限),且![]() 是线段
是线段![]() 的中点,过点
的中点,过点![]() 作x轴的垂线交C于另一点
作x轴的垂线交C于另一点![]() ,延长线
,延长线![]() 交C于点
交C于点![]() .
.
(i)设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,证明:
,证明:![]() ;
;
(ii)求直线![]() 的斜率的最小值.
的斜率的最小值.
【答案】(Ⅰ)![]() ;(Ⅱ)(i)见解析;(ii)
;(Ⅱ)(i)见解析;(ii)![]()
【解析】
(Ⅰ)根据抛物线焦点坐标求得![]() ,再利用离心率和
,再利用离心率和![]() 的关系求得
的关系求得![]() ,进而得到椭圆方程;(Ⅱ)(i)利用
,进而得到椭圆方程;(Ⅱ)(i)利用![]() 为线段
为线段![]() 中点表示出
中点表示出![]() 点坐标,再根据椭圆对称性得到
点坐标,再根据椭圆对称性得到![]() 点坐标;利用两点连线斜率公式表示出
点坐标;利用两点连线斜率公式表示出![]() 和
和![]() ,从而结论可证;(ii)将直线
,从而结论可证;(ii)将直线![]() 方程与椭圆方成立联立,利用韦达定理可用
方程与椭圆方成立联立,利用韦达定理可用![]() 和
和![]() 表示出
表示出![]() ,利用
,利用![]() 同理可求得
同理可求得![]() ,进而利用两点连线斜率公式写出所求斜率,结合基本不等式求出最小值.
,进而利用两点连线斜率公式写出所求斜率,结合基本不等式求出最小值.
(Ⅰ)![]() 抛物线
抛物线![]() 的焦点是
的焦点是![]()
![]()
![]() 且
且![]()
![]() ,
,![]()
![]() 椭圆
椭圆![]() 的方程
的方程![]()
(Ⅱ)(i)设![]() ,那么
,那么![]()
![]() 是线段
是线段![]() 的中点
的中点 ![]() ,
,![]()
![]() ,
,![]()
![]()
(ii)根据题意得:直线![]() 的斜率一定存在且
的斜率一定存在且![]()
设直线![]() 为
为![]() ,则直线
,则直线![]() 为
为![]()
联立 ,整理得:
,整理得:![]()
利用韦达定理可知:![]()
![]()
![]()
![]() 同理可得
同理可得![]()
![]()
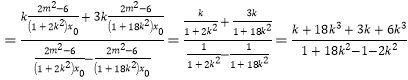
![]()
![]()
![]()
当且仅当![]() 即为
即为![]() 时,等号成立
时,等号成立
![]() 直线
直线![]() 斜率的最小值为
斜率的最小值为![]()


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,已知棱
中,已知棱![]() ,
,![]() ,
,![]() 两两垂直,长度分别为1,2,2.若
两两垂直,长度分别为1,2,2.若![]() (
(![]() ),且向量
),且向量![]() 与
与![]() 夹角的余弦值为
夹角的余弦值为![]() .
.
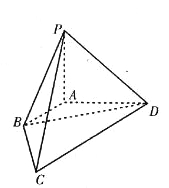
(1)求![]() 的值;
的值;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①离心率![]() ,②椭圆
,②椭圆![]() 过点
过点![]() ,③
,③![]() 面积的最大值为
面积的最大值为![]() ,这三个条件中任选一个,补充在下面(横线处)问题中,解决下面两个问题.
,这三个条件中任选一个,补充在下面(横线处)问题中,解决下面两个问题.
设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点,已知椭圆
两点,已知椭圆![]() 的短轴长为
的短轴长为![]() ,________.
,________.
(1)求椭圆![]() 的方程;
的方程;
(2)若线段![]() 的中垂线与
的中垂线与![]() 轴交于点
轴交于点![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产并销售某高科技产品,已知每年生产该产品的固定成本是800万元,生产成本e(单位;万元)与生产的产品件数x(单位:万件)的平方成正比;该产品单价p(单位:元)与生产的产品件数x满足![]() (b为常数),已知当该产品的单价为300元时,生产成本是1800万元,当单价为320元时,生产成本是200万元,且工厂生产的产品都可以销售完.
(b为常数),已知当该产品的单价为300元时,生产成本是1800万元,当单价为320元时,生产成本是200万元,且工厂生产的产品都可以销售完.
(1)每年生产该产品多少万件时,平均成本最低,最低为多少?
(2)若该工厂希望年利润不低于8200万元,则每年大约应该生产多少万件该产品?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的焦点坐标为![]() ,
,![]() ,过
,过![]() 垂直于长轴的直线交椭圆于
垂直于长轴的直线交椭圆于![]() 、
、![]() 两点,且
两点,且![]() .
.
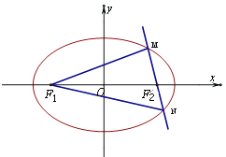
(Ⅰ)求椭圆的方程;
(Ⅱ)过![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() 、
、![]() ,则
,则![]() 的内切圆的面积是否存在最大值?若存在求出这个最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值?若存在求出这个最大值及此时的直线方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已数列![]() 的各项均为正整数,且满足
的各项均为正整数,且满足![]() ,又
,又![]() .
.
(1)求![]() 的值,猜想
的值,猜想![]() 的通项公式并用数学归纳法证明;
的通项公式并用数学归纳法证明;
(2)设![]() ,求
,求![]() 的值;
的值;
(3)设![]() ,是否存在最大的整数
,是否存在最大的整数![]() ,使得对任意
,使得对任意![]() ,均有
,均有![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com