
【题目】《算法统宗》全称《新编直指算法统宗》,是屮国古代数学名著,程大位著.书中有如下问题:“今有五人均银四十两,甲得十两四钱,戊得五两六钱.问:次第均之,乙丙丁各该若干?”意思是:有5人分40两银子,甲分10两4钱,戊分5两6钱,且相邻两项差相等,则乙丙丁各分几两几钱?(注:1两等于10钱)( )
A.乙分8两,丙分8两,丁分8两B.乙分8两2钱,丙分8两,丁分7两8钱
C.乙分9两2钱,丙分8两,丁分6两8钱D.乙分9两,丙分8两,丁分7两
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】詹姆斯·哈登(James Harden)是美国NBA当红球星,自2012年10月加盟休斯顿火箭队以来,逐渐成长为球队的领袖.2017-18赛季哈登当选常规赛MVP(最有价值球员).
年份 | 2012-13 | 2013-14 | 2014-15 | 2015-16 | 2016-17 | 2017-18 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
常规赛场均得分y | 25.9 | 25.4 | 27.4 | 29.0 | 29.1 | 30.4 |
(Ⅰ)根据表中数据,求y关于t的线性回归方程![]() (
(![]() ,
,![]()
![]() *);
*);
(Ⅱ)根据线性回归方程预测哈登在2019-20赛季常规赛场均得分.
(附)对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:![]() ,
,![]()
(参考数据![]() ,计算结果保留小数点后一位)
,计算结果保留小数点后一位)
查看答案和解析>>
科目:高中数学 来源: 题型:
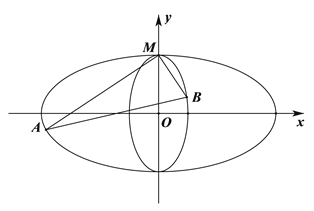
【题目】如图,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 与焦点在
与焦点在![]() 轴上的椭圆
轴上的椭圆![]() 都过点
都过点![]() ,中心都在坐标原点,且椭圆
,中心都在坐标原点,且椭圆![]() 与
与![]() 的离心率均为
的离心率均为![]() .
.
(Ⅰ)求椭圆![]() 与椭圆
与椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过点M的互相垂直的两直线分别与![]() ,
,![]() 交于点A,B(点A、B不同于点M),当
交于点A,B(点A、B不同于点M),当![]() 的面积取最大值时,求两直线MA,MB斜率的比值.
的面积取最大值时,求两直线MA,MB斜率的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有两个调查抽样:(1)某班为了了解班级学生在家表现情况决定从10名家长中抽取3名参加座谈会;(2)某研究部门在高考后从2000名学生(其中文科400名,理科1600名)中抽取200名考生作为样本调查数学学科得分情况.
给出三种抽样方法:Ⅰ.简单随机抽样法;Ⅱ.系统抽样法;Ⅲ.分层抽样法.
则问题(1)、(2)选择的抽样方法合理的是( )
A.(1)选Ⅲ,(2)选ⅠB.(1)选Ⅰ,(2)选Ⅲ
C.(1)选Ⅱ,(2)选ⅠD.(1)选Ⅲ,(2)选Ⅱ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了迎接全国文明城市复检,绵阳某中学组织了本校1000名学生进行社会主义核心价值观、文明常识等内容测试。统计测试成绩数据得到如图所示的频率分布直方图,已知![]() ,满分100分.
,满分100分.
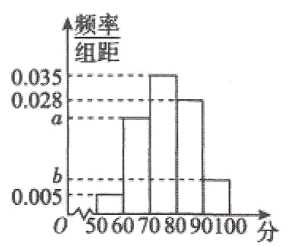
(1)求测试分数在![]() 的学生人数;
的学生人数;
(2)求这1000名学生测试成绩的平均数以及中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C的方程为![]() ,O为坐标原点,A为椭团的上顶点,
,O为坐标原点,A为椭团的上顶点,![]() 为其右焦点,D是线段
为其右焦点,D是线段![]() 的中点,且
的中点,且![]() .
.
(1)求椭圆C的方程;
(2)过坐标原点且斜率为正数的直线交椭圆C于P,Q两点,分别作![]() 轴,
轴,![]() 轴,垂足分别为E,F,连接
轴,垂足分别为E,F,连接![]() ,
,![]() 并延长交椭圆C于点M,N两点.
并延长交椭圆C于点M,N两点.
(ⅰ)判断![]() 的形状;
的形状;
(ⅱ)求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点P在曲线y=x2上,从原点向A(2,4)移动,如果直线OP,曲线y=x2及直线x=2所围成的面积分别记为S1、S2.
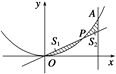
(1)当S1=S2时,求点P的坐标;
(2)当S1+S2有最小值时,求点P的坐标和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知袋子中放有大小和形状相同标号分别是0,1,2的小球若干,其中标号为0的小球1个,标号为1的小球2个,标号为2的小球n个.若从袋子中随机抽取1个小球,取到标号为2的小球的概率是![]() .
.
(1)求n的值
(2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球标号为a,第二次取出的球标号为b.
①记“![]() ”为事件A,求事件A的概率;
”为事件A,求事件A的概率;
②在区间![]() 内任取2个实数x,y,求事件“
内任取2个实数x,y,求事件“![]() 恒成立”的概率.
恒成立”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年10月5日, 美国NBA火箭队总经理莫雷公开发布涉港错误言论,中国公司与明星纷纷站出来抵制火箭队,随后京东、天猫、淘宝等中国电商平台全线下架了火箭队的所有商品,当天有大量网友关注此事,某网上论坛从关注此事跟帖中,随机抽取了100名网友进行调查统计,先分别统计他们在跟帖中的留言条数,再把网友人数按留言条数分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图;并将其中留言不低于40条的规定为“强烈关注”,否则为“一般关注”,对这100名网友进一步统计得到列联表的部分数据如下表:
,得到如图所示的频率分布直方图;并将其中留言不低于40条的规定为“强烈关注”,否则为“一般关注”,对这100名网友进一步统计得到列联表的部分数据如下表:
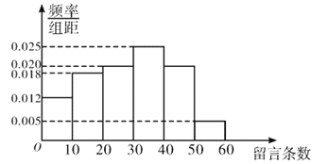
一般关注 | 强烈关注 | 合计 | |
男 | 60 | ||
女 | 5 | 40 | |
合计 | 100 |
(1)补全列联表中数据,并判断能否有![]() 的把握认为网友对此事件是否为“强烈关注”与性别有关?
的把握认为网友对此事件是否为“强烈关注”与性别有关?
(2)现已从男性网友中分层抽样选取了6人,再从这6人中随机选取2人,求这2人中至少有1人属于“强烈关注”的概率.
附: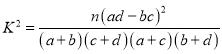 ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com