
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,已知a+b=5,c= ![]() ,且4sin2
,且4sin2 ![]() ﹣cos2C=
﹣cos2C= ![]()
(1)求角C的大小;
(2)求△ABC的面积.
【答案】
(1)解:∵A+B+C=180°,由 ![]() ,得
,得 ![]() ,
,
∴ ![]() ,
,
整理得:4cos2C﹣4cosC+1=0,
解得: ![]() ,
,
由于:0<C<π,
可得:C= ![]() .
.
(2)解:∵由余弦定理可得:c2=a2+b2﹣2abcosC,即:7=a2+b2﹣ab,
∴7=(a+b)2﹣3ab,
∵由条件a+b=5,
∴可得:7=25﹣3ab,解得:ab=6,
∴ ![]() .
.
【解析】(1)由三角函数恒等变换的应用化简已知等式可得4cos2C﹣4cosC+1=0,可求 ![]() ,结合范围0<C<π,即可得解C的值.(2)由余弦定理可得7=(a+b)2﹣3ab,结合条件a+b=5,可求ab的值,进而利用三角形面积公式即可计算得解.
,结合范围0<C<π,即可得解C的值.(2)由余弦定理可得7=(a+b)2﹣3ab,结合条件a+b=5,可求ab的值,进而利用三角形面积公式即可计算得解.
【考点精析】解答此题的关键在于理解余弦定理的定义的相关知识,掌握余弦定理:![]() ;
;![]() ;
;![]() .
.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:a1=﹣13,a6+a8=﹣2,且an﹣1=2an﹣an+1(n≥2),则数列{ ![]() }的前13项和为( )
}的前13项和为( )
A.![]()
B.﹣ ![]()
C.![]()
D.﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若f(x)是奇函数,且在(0,+∞)上是增函数,又f(﹣3)=0,则(x﹣1)f(x)<0的解是( )
A.(﹣3,0)∪(1,+∞)
B.(﹣3,0)∪(0,3)
C.(﹣∞,﹣3)∪(3,+∞)
D.(﹣3,0)∪(1,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知六棱锥P﹣ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB则下列结论正确的是( ) 
A.PB⊥AD
B.平面PAB⊥平面PBC
C.直线BC∥平面PAE
D.直线PD与平面ABC所成的角为45°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A、B分别为双曲线 ![]() 的左右顶点,双曲线的实轴长为4
的左右顶点,双曲线的实轴长为4 ![]() ,焦点到渐近线的距离为
,焦点到渐近线的距离为 ![]() .
.
(1)求双曲线的方程;
(2)已知直线 ![]() 与双曲线的右支交于M、N两点,且在双曲线的右支上存在点D,使
与双曲线的右支交于M、N两点,且在双曲线的右支上存在点D,使 ![]() ,求t的值及点D的坐标.
,求t的值及点D的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,我艇在A处发现一走私船在方位角45°且距离为12海里的B处正以每小时10海里的速度向方位角105°的方向逃窜,我艇立即以14海里/小时的速度追击,求我艇追上走私船所需要的最短时间. 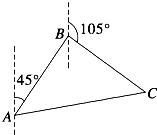
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】调查某车间20名工人的年龄,第i名工人的年龄为ai,具体数据见表:
i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
ai | 29 | 28 | 30 | 19 | 31 | 28 | 30 | 28 | 32 | 31 | 30 | 31 | 29 | 29 | 31 | 32 | 40 | 30 | 32 | 30 |
(1)作出这20名工人年龄的茎叶图;
(2)求这20名工人年龄的众数和极差;
(3)执行如图所示的算法流程图(其中 ![]() 是这20名工人年龄的平均数),求输出的S值.
是这20名工人年龄的平均数),求输出的S值. 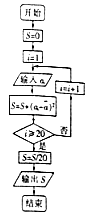
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com