
若函数 的定义域为
的定义域为 ,且满足
,且满足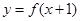 为 奇函数,
为 奇函数,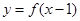 为偶函数,则下列说法中一定正确的有
为偶函数,则下列说法中一定正确的有
(1) 的图像关于直线
的图像关于直线 对称
对称
(2) 的周期为
的周期为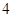
(3)
(4) 在
在 上只有一个零点
上只有一个零点

【解析】
试题分析:因为,函数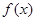 的定义域为
的定义域为 ,且满足
,且满足 为 奇函数,
为 奇函数, 为偶函数,所以f(-x+1)=-f(x+1) .......(1);f(x-1)=f(-x-1).......(2)。
为偶函数,所以f(-x+1)=-f(x+1) .......(1);f(x-1)=f(-x-1).......(2)。
由(1) 得f(x+1)=-f(-x+1) ,故 ;
;
由(2) 得f(x-1)=f(-x-1),故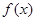 的图像关于直线
的图像关于直线 对称;(1)正确。由此可知,函数
对称;(1)正确。由此可知,函数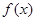 在
在 要吗没零点,要吗不只一个零点;(4)不正确。
要吗没零点,要吗不只一个零点;(4)不正确。
由①令-x+1=t得:f(t)=-f(2-t)…………③;②令-x-1=t得:f(t)= f(-2-t)………④;
由③、④得f(2-t)=- f(-2-t)由此令-2-t=m得f(4+m) =-f(m),
所以,f(8+m) =-f(m+4)= f(m),函数f(x)的周期为8,(2)不正确。
所以 ,(3)正确。
,(3)正确。
综上知,答案为(1)(3)
考点:本题主要考查函数的奇偶性、周期性、对称性。
点评:中档题,本题比较典型,综合考查了函数的奇偶性、周期性、对称性,有一定难度,需要灵活运用“代换的方法”,寻求所需条件、结论。


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源:2016届北京市海淀区高一上学期期末统考数学试卷(解析版) 题型:解答题
已知函数 的定义域为
的定义域为 ,且
,且 的图象连续不间断. 若函数
的图象连续不间断. 若函数 满足:对于给定的
满足:对于给定的 (
( 且
且 ),存在
),存在 ,使得
,使得 ,则称
,则称 具有性质
具有性质 .
.
(Ⅰ)已知函数 ,
, ,判断
,判断 是否具有性质
是否具有性质 ,并说明理由;
,并说明理由;
(Ⅱ)已知函数 若
若 具有性质
具有性质 ,求
,求 的最大值;
的最大值;
(Ⅲ)若函数 的定义域为
的定义域为 ,且
,且 的图象连续不间断,又满足
的图象连续不间断,又满足 ,
,
求证:对任意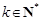 且
且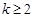 ,函数
,函数 具有性质
具有性质 .
.
查看答案和解析>>
科目:高中数学 来源:2014届山东省高一3月月考数学试卷(解析版) 题型:填空题
若函数 的定义域为
的定义域为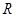 ,且存在常数
,且存在常数 ,对任意
,对任意 ,有
,有 ,则称
,则称 为
为 函数。给出下列函数:①
函数。给出下列函数:① ,②
,② ,③
,③ ,④
,④ 是定义在
是定义在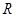 上的奇函数,且满足对一切实数
上的奇函数,且满足对一切实数 均有
均有 ,⑤
,⑤ ,其中是
,其中是 函数的有____________________。
函数的有____________________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com