
【题目】如图,在底面为直角梯形的四棱锥![]() 中,
中,![]() ,
,![]()
![]() 平面
平面![]() ,
,![]() ,
,![]() .
.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小.
的大小.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连接![]() 交于
交于![]() ,由
,由![]() 平面
平面![]() ,可得
,可得![]() ,
,![]() ,
,![]() 可得
可得![]() ,
,![]() ,
,![]() ,即
,即![]() ,从而根据线面垂直的判定定理可得
,从而根据线面垂直的判定定理可得![]() 平面
平面![]() ;(2) 连接
;(2) 连接![]() ,
,![]() 平面
平面![]() .
.![]() ,
,![]() .
.![]() 为二面角
为二面角![]() 的平面角,根据直角三角形的性质可得
的平面角,根据直角三角形的性质可得![]() ,进而可得二面角
,进而可得二面角![]() 的大小.
的大小.
试题解析:(1)连接![]() 交于
交于![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.![]() .
.

又![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() ,即
,即![]() .
.
又![]() .
.![]() 平面
平面![]() .
.
(2)连接![]() .
.![]() 平面
平面![]() .
.![]() ,
,![]() .
.![]() 为二面角
为二面角![]() 的平面角.
的平面角.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 二面角
二面角![]() 的大小为
的大小为![]() .
.
【方法点晴】本题主要考查线面垂直的判定定理及二面角的求法,属于难题.解答空间几何体中垂直关系时,一般要根据已知条件把空间中的线线、线面、面面之间垂直关系进行转化,转化时要正确运用有关的定理,找出足够的条件进行推理;证明直线和平面垂直的常用方法有:(1)利用判定定理;(2)利用判定定理的推论![]() ;(3)利用面面平行的性质
;(3)利用面面平行的性质![]() ;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.
;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某学校为了加强学生数学核心素养的培养,锻炼学生自主探究学习的能力,他们以函数![]() 为基本素材,研究该函数的相关性质,取得部分研究成果如下:
为基本素材,研究该函数的相关性质,取得部分研究成果如下:
①同学甲发现:函数![]() 的定义域为
的定义域为![]() ;
;
②同学乙发现:函数![]() 是偶函数;
是偶函数;
③同学丙发现:对于任意的![]() 都有
都有![]() ;
;
④同学丁发现:对于任意的![]() ,都有
,都有![]() ;
;
⑤同学戊发现:对于函数![]() 定义域中任意的两个不同实数
定义域中任意的两个不同实数![]() ,总满足
,总满足![]() .
.
其中所有正确研究成果的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
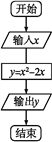
【题目】求函数y=![]() 的值的程序框图如图所示.
的值的程序框图如图所示.
(1)指出程序框图中的错误,并写出算法;
(2)重新绘制解决该问题的程序框图,并回答下面提出的问题.
①要使输出的值为正数,输入的x的值应满足什么条件?
②要使输出的值为8,输入的x值应是多少?
③要使输出的y值最小,输入的x值应是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义“三角恋写法”为“三个人之间写信,每人给另外两人之一写一封信,且任意两个人不会彼此给对方写信”,若五个人a,b,c,d,e中的每个人都恰给其余四人中的某一个人写了一封信,则不出现“三角恋写法”写法的写信情况的种数为( )
A.704
B.864
C.1004
D.1014
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级举行一次知识竞赛活动,活动分为初赛和决赛两个阶段、现将初赛答卷成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表.
分数(分数段) | 频数(人数) | 频率 |
[60,70) | ① | 0.16 |
[70,80) | 22 | ② |
[80,90) | 14 | 0.28 |
[90,100) | ③ | ④ |
合计 | 50 | 1 |
(1)填充频率分布表中的空格(在解答中直接写出对应空格序号的答案);
(2)决赛规则如下:参加决赛的每位同学依次口答4道小题,答对2道题就终止答题,并获得一等奖.如果前三道题都答错,就不再答第四题.某同学进入决赛,每道题答对的概率P的值恰好与频率分布表中不少于80分的频率的值相同. ①求该同学恰好答满4道题而获得一等奖的概率;
②记该同学决赛中答题个数为X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,底面△ABC是等边三角形,侧面AA1B1B为正方形,且AA1⊥平面ABC,D为线段AB上的一点. 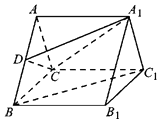
(Ⅰ)若BC1∥平面A1CD,确定D的位置,并说明理由;
(Ⅱ)在(Ⅰ)的条件下,求二面角A1D﹣C﹣BC1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣5|﹣|x﹣2|.
(1)若x∈R,使得f(x)≤m成立,求m的范围;
(2)求不等式x2﹣8x+15+f(x)≤0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知x∈[﹣1,0],θ∈[0,2π),二元函数 ![]() 取最小值时,x=x0 , θ=θ0则( )
取最小值时,x=x0 , θ=θ0则( )
A.4x0+θ0=0
B.4x0+θ0<0
C.4x0+θ0>0
D.以上均有可能.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com