
【题目】某钢厂打算租用![]() ,
,![]() 两种型号的火车车皮运输900吨钢材,
两种型号的火车车皮运输900吨钢材,![]() ,
,![]() 两种车皮的载货量分别为36吨和60吨,租金分别为1.6万元/个和2.4万元/个,钢厂要求租车皮总数不超过21个,且
两种车皮的载货量分别为36吨和60吨,租金分别为1.6万元/个和2.4万元/个,钢厂要求租车皮总数不超过21个,且![]() 型车皮不多于
型车皮不多于![]() 型车皮7个,分别用
型车皮7个,分别用![]() ,
,![]() 表示租用
表示租用![]() ,
,![]() 两种车皮的个数.
两种车皮的个数.
(1)用![]() ,
,![]() 列出满足条件的数学关系式,并画出相应的平面区域;
列出满足条件的数学关系式,并画出相应的平面区域;
(2)分别租用![]() ,
,![]() 两种车皮的个数是多少时,才能使得租金最少?并求出此最小租金.
两种车皮的个数是多少时,才能使得租金最少?并求出此最小租金.
科目:高中数学 来源: 题型:
【题目】宿州市某登山爱好者为了解山高y(百米)与气温x(℃)之间的关系,随机统计了4次山高与相应的气温,并制作了对照表,由表中数据,得到线性回归方程为y=﹣2x+a,由此估计山高为72(百米)处的气温为( )
气温x(℃) | 18 | 13 | 10 | ﹣1 |
山高y(百米) | 24 | 34 | 38 | 64 |
A.﹣10
B.﹣8
C.﹣6
D.﹣4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() ,
, ![]() ,
, ![]() 分别为椭圆的右顶点、上顶点和右焦点,且
分别为椭圆的右顶点、上顶点和右焦点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() :
: ![]() 被圆
被圆![]() :
: ![]() 所截得的弦长为
所截得的弦长为![]() ,若直线
,若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=x2+ax+3,已知不等式f(x)<0的解集为{x|1<x<3}.
(1)求a;
(2)若不等式f(x)≥m的解集是R,求实数m的取值范围;
(3)若f(x)≥nx对任意的实数x≥1成立,求实数n的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断居民户是否小康的一个重要指标是居民户的年收入,某市从辖区内随机抽取100个居民户,对每个居民户的年收入与年结余的情况进行分析,设第i个居民户的年收入xi(万元),年结余yi(万元),经过数据处理的: ![]() =400,
=400, ![]() =100,
=100, ![]() =900,
=900, ![]() =2850.
=2850.
(1)已知家庭的年结余y对年收入x具有线性相关关系,求线性回归方程;
(2)若该市的居民户年结余不低于5万,即称该居民户已达小康生活,请预测居民户达到小康生活的最低年收入应为多少万元? 附:在y=bx+a中,b= 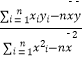 ,a=
,a= ![]() ,其中
,其中 ![]() ,
, ![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)的一个顶点为A(0,1),离心率为
=1(a>b>0)的一个顶点为A(0,1),离心率为 ![]() ,过点B(0,﹣2)及左焦点F1的直线交椭圆于C,D两点,右焦点设为F2 .
,过点B(0,﹣2)及左焦点F1的直线交椭圆于C,D两点,右焦点设为F2 .
(1)求椭圆的方程;
(2)求△CDF2的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|< ![]() )的最小正周期为2 π,最小值为﹣2,且当x=
)的最小正周期为2 π,最小值为﹣2,且当x= ![]() 时,函数取得最大值4. (Ⅰ)求函数 f(x)的解析式;
时,函数取得最大值4. (Ⅰ)求函数 f(x)的解析式;
(Ⅱ)求函数f(x)的单调递增区间;
(Ⅲ)若当x∈[ ![]() ,
, ![]() ]时,方程f(x)=m+1有解,求实数m的取值范围.
]时,方程f(x)=m+1有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四棱柱ABCD﹣A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC 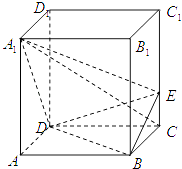
(1)证明:A1C⊥平面BED;
(2)求二面角A1﹣DE﹣B的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com