
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据三角函数的图象和性质,可得命题p:a=1+4k,k∈Z;根据直线与圆的位置关系,可得命题q:a=1,或a=9,进而根据充要条件的定义,可得答案.
解答 解:当$\frac{π}{2}$x=$\frac{π}{2}$+2kπ,k∈Z,即x=1+4k,k∈Z时,函数取到最大值;
故命题p:a=1+4k,k∈Z;
若直线x-y+2=0与圆(x-3)2+(y-a)2=8相切,
则$\frac{|3-a+2|}{\sqrt{2}}$=2$\sqrt{2}$,
解得:a=1,或a=9,
即命题q:a=1,或a=9,
故p是q的必要不充分条件,
故选:B
点评 本题考查的知识点是充要条件的定义,函数的最值及其几何意义,直线与圆的位置关系,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | {x|x<-1或x>2} | B. | {x|x<-2或x>1} | C. | {x|-2<x<1} | D. | {x|-1<x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.897 | 10.828 |
| 对服务好评 | 对服务不满意 | 合计 | |
| 对商品好评 | a=80 | b=40 | 120 |
| 对商品不满意 | c=70 | d=10 | 80 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $-\frac{1}{3}$ | C. | $-\frac{3}{4}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
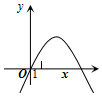 已知二次函数y=ax2+bx+c=0(a≠0)的图象如图所示,记p=|a-b+c|+|2a+b|,q=|a+b+c|+|2a-b|,则( )
已知二次函数y=ax2+bx+c=0(a≠0)的图象如图所示,记p=|a-b+c|+|2a+b|,q=|a+b+c|+|2a-b|,则( )| A. | p>q | B. | p=q | ||
| C. | p<q | D. | p,q大小关系不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
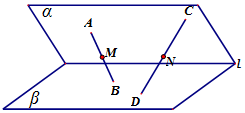 已知平面α∩平面β=直线l,点A,C∈α,点B,D∈β,且A,B,C,D∉l,点M,N分别是线段AB,CD的中点.( )
已知平面α∩平面β=直线l,点A,C∈α,点B,D∈β,且A,B,C,D∉l,点M,N分别是线段AB,CD的中点.( )| A. | 当|CD|=2|AB|时,M,N不可能重合 | |
| B. | M,N可能重合,但此时直线AC与l不可能相交 | |
| C. | 当直线AB,CD相交,且AC∥l时,BD可与l相交 | |
| D. | 当直线AB,CD异面时,MN可能与l平行 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com