
【题目】已知函数![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)画出![]() 图像,并写出单调递增区间(不需要说明理由);
图像,并写出单调递增区间(不需要说明理由);
(3)若![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)图像见解析,(-∞,2)和(4,∞)(3)(8, 6+2
;(2)图像见解析,(-∞,2)和(4,∞)(3)(8, 6+2![]() )
)
【解析】
(1)利用f(4)=0,列出方程即可求实数m的值;
(2)化简函数的解析式,得到分段函数,然后作出函数f(x)的图象,根据图象直接指出f(x)的单调递减区间;
(3)借助函数图象的对称性,转化为求解c的取值范围.
(1)∵![]() =x∣m-x∣,且
=x∣m-x∣,且![]() )=0
)=0
∴ 4∣m-4∣=0
∴m=4
(2)f(x)=x|x﹣4|=![]() ,
,
f(x)的图象如图所示.
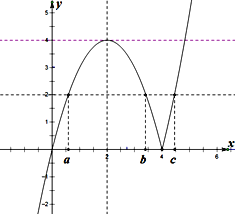
其单调增区间为:(-∞,2)和(4,∞)
(3)由图知: a+b=4为定值,即a+b+c的取值范围即为4+c的取值范围,
又∵当y=4时,x=2或x=2+2![]() ,
,
故c的取值范围为(4,2+2![]() ),
),
所以a+b+c的取值范围为(8, 6+2![]() )
)


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
: ![]() 的离心率
的离心率![]() ,且椭圆
,且椭圆![]() 上一点
上一点![]() 到点
到点![]() 的距离的最大值为
的距离的最大值为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() ,
, ![]() 为抛物线
为抛物线![]() :
: ![]() 上一动点,过点
上一动点,过点![]() 作抛物线
作抛物线![]() 的切线交椭圆
的切线交椭圆![]() 于
于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示. 
(1)求f(x)的解析式,并求函数f(x)在[﹣ ![]() ,
, ![]() ]上的值域;
]上的值域;
(2)在△ABC中,AB=3,AC=2,f(A)=1,求sin2B.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,空间四边形ABCD的对棱AD、BC成600的角,且AD=BC=a,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H.
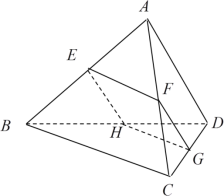
(1)求证:四边形EFGH为平行四边形;
(2)E在AB的何处时截面EFGH的面积最大?最大面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为{x|x≠0}的偶函数f(x),其导函数为f′(x),对任意正实数x满足xf′(x)>﹣2f(x),若g(x)=x2f(x),则不等式g(x)<g(1﹣x)的解集是( )
A.( ![]() ,+∞)
,+∞)
B.(﹣∞, ![]() )
)
C.(﹣∞,0)∪(0, ![]() )
)
D.(0, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品在近30天内每件的销售价格P元和时间t(t∈N)的关系如图所示.
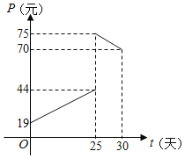
(1)请确定销售价格P(元)和时间t(天)的函数解析式;
(2)该商品的日销售量Q(件)与时间t(天)的关系是:Q=﹣t+40(0≤t≤30,t∈N),求该商品的日销售金额y(元)与时间t(天)的函数解析式;
(3)求该商品的日销售金额y(元)的最大值,并指出日销售金额最大的一天是30天中的哪一天?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() :若
:若![]() ,则
,则![]() ,下列说法正确的是( )
,下列说法正确的是( )
A. 命题![]() 的否命题是“若
的否命题是“若![]() ,则
,则![]() ”
”
B. 命题![]() 的逆否命题是“若
的逆否命题是“若![]() ,则
,则![]() ”
”
C. 命题![]() 是真命题
是真命题
D. 命题![]() 的逆命题是真命题
的逆命题是真命题
【答案】D
【解析】A. 命题![]() 的否命题是若
的否命题是若![]()
B. 命题![]() 的逆否命题是“若
的逆否命题是“若![]() ,则
,则![]()
![]()
C. 命题![]() 是假命题,比如当x=-3,就不满足条件,故选项不正确.
是假命题,比如当x=-3,就不满足条件,故选项不正确.
D. 命题![]() 的逆命题是若
的逆命题是若![]() 是真命题.
是真命题.
故答案为:D.
【题型】单选题
【结束】
9
【题目】“双曲线的方程为![]() ”是“双曲线的渐近线方程为
”是“双曲线的渐近线方程为![]() ”的( )
”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com