【答案】
分析:首先分析一元二次方程有实根的条件,得到a
2≥b
2.
(1)本题是一个古典概型,试验发生包含的基本事件可以通过列举得到结果数,满足条件的事件在前面列举的基础上得到结果数,求得概率.
(2)本题是一个几何概型,试验的全部结束所构成的区域为{(a,b)|0≤a≤2,0≤b≤3},满足条件的构成事件A的区域为{(a,b)|0≤a≤2,0≤b≤3,a≥b},根据概率等于面积之比,得到概率.
解答: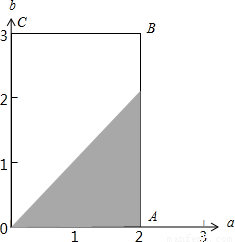
解:方程有实根时,△=(2a)
2-4b
2≥0,即a
2≥b
2.记方程x
2+2ax+b
2=0有实根的事件为A.
(1)当a∈{-2,-1,0,1,2},b∈{0,1,2,3}时,a与b的所有组合为(第一个数为a的值,第二个数为b的值):
(-2,0),(-2,1),(-2,2),(-2,3),(-1,0),(-1,1),(-1,2),(-1,3),(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,2),(1,3),(2,0),(2,1),(2,2),(2,3),共20组,即基本事件有20个,由于a在{-2,-1,0,1,2}里取是随机的,b在{0,1,2,3}里取是随机的,所以上述20个事件是等可能性的.
又因为满足条件a
2≥b
2的有:(-2,0),(-2,1),(-2,2),(-1,0),(-1,1),(0,0),(1,0),(1,1),(2,0),(2,1),(2,2)共11个,即事件A包含了11个基本事件,
所以P(A)=
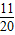
,
所以,方程x
2+2ax+b
2=0有实根的概率为
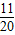
.
(2)设点M的坐标为(a,b),由于a∈[0,2],b∈[0,3],所以,所有的点M对构成坐标平面上一个区域(如图6中的矩形OABC),即所有的基本事件构成坐标平面上的区域OABC,其面积为2×3=6.
由于a在[0,2]上随机抽取,b在[0,3]上随机抽取,
所以,组成区域ABCD的所有基本事件是等可能性的.
又由于满足条件0≤a≤2,且0≤b≤3,且a
2≥b
2,即a≥b的平面区域如图6中阴影部分所示,其面积为

×2×2=2,
所以,事件A组成平面区域的面积为4,所以P(A)=

=

.
所以,方程x
2+2ax+b
2=0有实根的概率为

.
点评:本题考查古典概型及其概率公式,考查几何概型及其概率公式,本题把两种概率放在一个题目中进行对比,得到两种概率的共同之处和不同点.

 解:方程有实根时,△=(2a)2-4b2≥0,即a2≥b2.记方程x2+2ax+b2=0有实根的事件为A.
解:方程有实根时,△=(2a)2-4b2≥0,即a2≥b2.记方程x2+2ax+b2=0有实根的事件为A.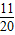 ,
,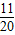 .
. ×2×2=2,
×2×2=2, =
= .
. .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案