练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某大学的名同学准备拼车去旅游，其中大一、大二、大三、大四每个年级各两名，分乘甲、乙两辆汽车.每车限坐名同学(乘同一辆车的名同学不考虑位置)，其中大一的孪生姐妹需乘同一辆车，则乘坐甲车的名同学中恰有名同学是来自于同一年级的乘坐方式共有_______种（有数字作答）.

    【答案】24

    【解析】试题分析：由题意，第一类，大一的孪生姐妹在甲车上，甲车上剩下两个要来自不同的年级，从三个年级中选两个为，然后分别从选择的年级中再选择一个学生，为，故有 =3×2×2=12种．

    第二类，大一的孪生姐妹不在甲车上，则从剩下的3个年级中选择一个年级的两名同学在甲车上，为，然后再从剩下的两个年级中分别选择一人（同第一类情况），这时共有 =3×2×2=12种

    因此共有24种不同的乘车方式，故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图,正方体ABCD-A1B1C1D1中,P,M,N分别为棱DD1,AB,BC的中点.

    (1)求二面角B1-MN-B的正切值.

    (2)求证:PB⊥平面MNB1.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

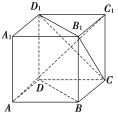
    【题目】【2017唐山模拟】如图，ABCDA1B1C1D1为正方体，连接BD，AC1，B1D1，CD1，B1C，现有以下几个结论：①BD∥平面CB1D1；②AC1⊥平面CB1D1；③AC1与底面ABCD所成角的正切值是；④CB1与BD为异面直线，其中所有正确结论的序号为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】社会调查人员希望从对人群的随机抽样调查中得到对他们所提问题诚实的回答，但是被采访者常常不愿意如实做出应答．

    1965年Stanley·L.Warner发明了一种应用概率知识来消除这种不愿意情绪的方法．Warner的随机化应答方法要求人们随机地回答所提问题中的一个，而不必告诉采访者回答的是哪个问题，两个问题中有一个是敏感的或者是令人为难的，另一个是无关紧要的，这样应答者将乐意如实地回答问题，因为只有他知道自己回答的是哪个问题．

    假如在调查运动员服用兴奋剂情况的时候，无关紧要的问题是：你的身份证号码的尾数是奇数吗；敏感的问题是：你服用过兴奋剂吗．然后要求被调查的运动员掷一枚硬币，如果出现正面，就回答第一个问题，否则回答第二个问题．

    例如我们把这个方法用于200个被调查的运动员，得到56个“是”的回答，请你估计这群运动员中大约有百分之几的人服用过兴奋剂．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝xln x－(x－1)(ax－a＋1)(a∈R)．

    (1)若a＝0，判断函数f(x)的单调性；

    (2)若x>1时，f(x)<0恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某高校在2011年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组：第1组[75，80)，第2组[80，85)，第3组[85，90)，第4组[90，95)，第5组[95，100]得到的频率分布直方图如图所示．

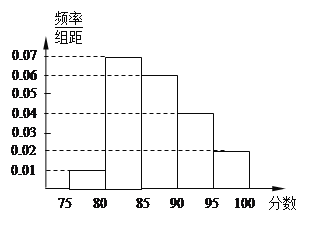
    （Ⅰ）分别求第3，4，5组的频率；

    （Ⅱ）若该校决定在笔试成绩高的第3，4，5组中用分层抽样抽取6名学生进入第二轮面试，求第3，4，5组每组各抽取多少名学生进入第二轮面试?

    （Ⅲ）在(Ⅱ)的前提下，学校决定在这6名学生中随机抽取2名学生接受甲考官的面试，求第4组至少有一名学生被甲考官面试的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设 ，函数

    （1）若 在 上单调递增，求 的取值范围；

    （2）记 为 在 上的最大值，求 的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知△ABC的三个内角A、B、C所对的边分别是a、b、c，向量m＝(cos B，cos C)，n＝(2a＋c，b)，且m⊥n.

    (1)求角B的大小；

    (2)若b＝，求a＋c的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在正方体ABCD-A1B1C1D1中，M，N，Q分别是棱D1C1，A1D1，BC的中点，P在对角线BD1上，且BP=BD1，给出下面四个命题：

    (1)MN∥平面APC；(2)C1Q∥平面APC；(3)A，P，M三点共线；(4)平面MNQ∥平面APC.正确的序号为　(　　)

    A. (1)(2) B. (1)(4) C. (2)(3) D. (3)(4)

    查看答案和解析>>

    同步练习册答案