练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    (1)已知(1+x)+(1+x)2+…+(1+x)n=a0+a1x+…+anxn,若a1+a2+…+an-1=509-n,求自然数n的值;

    (2)若(1-2x)6=a0+a1x+a2x2+…+a6x6,求|a0|+|a1|+…+|a6|的值;

    (3)若(x+2)8-(x+2)7+…+(-1)r·(x+2)8-r+…+1=a8(x+2)8+a7(x+2)7+…+a1(x+2)+a0,求a0+a1+…+a8的值.

    解:(1)令x=1,有2+22+…+2n=a0+a1+…+an.

        由已知得=a0+509-n+an.

    ∵a0=n,a1=1,

    ∴2n+1-2=n+509-n+1=510.

    ∴2n+1=512.

    ∴n=8.

    (2)设x=1,有a0+a1+a2+…+a6=1,

        令x=-1,有a0-a1+a2-a3+…+a6=36=729,两式相加

        得a0+a2+a4+a6=365,两式相减得a1+a3+a5=-364.

    ∴|a0|+|a1|+…+|a6|=a0-a1+a2-a3+a4-a5+a6=365+364=729.

        此题亦可这样解:

        由于求的是各项系数的绝对值之和,易知它与(1+2x)6的系数和相同,令x=-1,即有|a0|+|a1|+…+|a6|=36=729.

    (3)原式左边=［(x+2)-1］8=(x+1)8.

        由已知令x=-1,得a0+a1+a2+…+a8=08=0.

    点评:关于二项展开式的系数和的问题,根本思想是利用二项展开式是恒等式再使用赋值法去处理,利用赋值法可以得出很多关于组合数的恒等式,其中第(3)小题说明既要会展开二项式,又要会逆向使用二项式定理,还要正确赋值.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知定义域为[0，1]的函数f（x）同时满足：
    ①对于任意的x∈[0，1]，总有f（x）≥0；
    ②f（1）=1；
    ③若x1≥0，x2≥0，x1+x2≤1，则有f（x1+x2）≥f（x1）+f（x2）．
    （1）求f（0）的值；
    （2）求f（x）的最大值；
    （3）若对于任意x∈[0，1]，总有4f2（x）-4（2-a）f（x）+5-4a≥0成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出下列四个命题：
    ①已知f(x)+2f(
    1
    x
    )=3x    ，则函数g（x）=f（2x）在（0，1）上有唯一零点；
    ②对于函数f(x)=x
    1
    2
    的定义域中任意的x1、x2（x1≠x2）必有f(
    x1+x2
    2
    )＜
    f(x1)+f(x2)
    2
    ；
    ③已知f（x）=|2-x+1-1|，a＜b，f（a）＜f（b），则必有0＜f（b）＜1；
    ④已知f（x）、g（x）是定义在R上的两个函数，对任意x、y∈R满足关系式f（x+y）+f（x-y）=2f（x）•g（y），且f（0）=0，但x≠0时f（x）•g（x）≠0．则函数f（x）、g（x）都是奇函数．
    其中正确命题的序号是
    ①③
    ①③
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (1)已知函数f(x)=x2,g(x)为一次函数，且为增函数，若f［g(x)］=4x2-20x+15,求g(x)的解析式;

    (2)已知af(x)+bf()=cx(a、b、c∈R,ab≠0,a2≠b2),求f(x);

    (3)f(x)是R上的奇函数，且x∈(-∞,0)时，f(x)=x2+2x,求f(x);

    (4)某工厂生产一种机器的固定成本为5 000元，且每生产100部，需要增加投入2 500元，对销售市场进行调查后得知，市场对此产品的需求量为每年500部，已知销售收入的函数为H(x)=500x-x2,其中x是产品售出的数量，且0≤x≤500.若x为年产量，y表示利润，求y=f(x)的解析式.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (1)已知f(x-3)=x2+3x+1,求f(x)的解析式;

    (2)已知f(x)满足f(x-)=x2+,求函数f(x)的解析式;

    (3)已知函数f(x)是一次函数,且f［f(x)］=4x+1,求函数f(x)的解析式.

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年山东省潍坊市高三（上）12月统考数学试卷（解析版） 题型：解答题

    已知函数f（x）=ex+ax，g（x）=exlnx．（e≈2.71828）
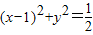    （I）设曲线y=f（x）在点（1，f（1））x=1处的切线为l，若l与圆相切，求a的值；
    （II）若对于任意实数x≥0，f（x）＞0恒成立，试确定实数a的取值范围；
    （III）当a=-1时，是否存在实数x∈[1，e]，使曲线C：y=g（x）-f（x）在点x=x处的切线与Y轴垂直？若存在，求出x的值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案