已知集合A={x|-1≤x≤0}，集合B={x|ax+b•2x-1＜0，0≤a≤2，1≤b≤3}．
（1）若a，b∈N，求A∩B≠∅的概率；
（2）若a，b∈R，求A∩B=∅的概率．
解：（1）因为a，b∈N，（a，b）可取（0，1），（0，2），（0，3），（1，1），（1，2），（1，3），（2，1），（2，2），（2，3）共9组．
令函数f（x）=ax+b•2
x-1，x∈[-1，0]，则f′（x）=a+bln2•2
x．
因为a∈[0，2]，b∈[1，3]，所以f′（x）＞0，即f（x）在[-1，0]上是单调递增函数．
f（x）在[-1，0]上的最小值为-a+
-1．要使A∩B≠∅，只需-a+
-1＜0，
即2a-b+2＞0．所以（a，b）只能取（0，1），（1，1），（1，2），（1，3），（2，1），（2，2），（2，3）7组．
所以A∩B≠∅的概率为
．
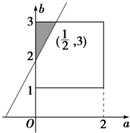
（2）因为a∈[0，2]，b∈[1，3]，
所以（a，b）对应的区域为边长为2的正方形（如图），面积为4．
由（1）可知，要使A∩B=∅，
只需f（x）
min=-a+
-1≥0?2a-b+2≤0，
所以满足A∩B=∅的（a，b）对应的区域是如图阴影部分．
所以S
阴影=
×1×
=
，所以A∩B=∅的概率为：P=
．
分析：（1）本小题是古典概型问题，欲求A∩B≠∅的概率，只须求出满足：“使A∩B≠∅”的事件空间中元素有多少个，再将求得的值与抽取的全部结果的个数求比值即得．
（2）本小题是几何概型问题，欲求A∩B=∅的概率，只须求出满足A∩B=∅的（a，b）对应的区域的面积，再将求得的面积值与整个区域的面积求比值即得．
点评：本小题主要考查古典概型、几何概型等基础知识．古典概型与几何概型的主要区别在于：几何概型是另一类等可能概型，它与古典概型的区别在于试验的结果不是有限个，简单地说，如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概率模型，简称为几何概型．
