
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
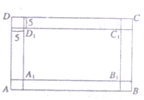 某市政府为了打造宜居城市,计划在公园内新建一个如图所示的矩形ABCD的休闲区,内不是矩形景观区A1B1C1D1,景观区四周是人行道,已知景观区的面积为8000平方米,人行道的宽为5米(如图所示).
某市政府为了打造宜居城市,计划在公园内新建一个如图所示的矩形ABCD的休闲区,内不是矩形景观区A1B1C1D1,景观区四周是人行道,已知景观区的面积为8000平方米,人行道的宽为5米(如图所示).查看答案和解析>>
科目:高中数学 来源: 题型:
 已知直线l过点P(3,2).
已知直线l过点P(3,2).查看答案和解析>>
科目:高中数学 来源: 题型:
| 60岁以下 | 60岁以上 | 总计 | |
| 看生产日期与保质期 | 50 | 30 | 80 |
| 不看生产日期与保质期 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com