
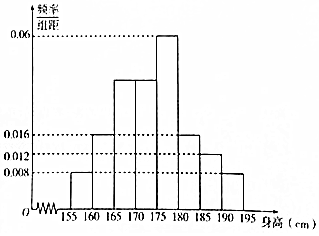
 从某校高一年级1000名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米到195厘米之间,将测量结果分为八组:第一组[155,160),第二组[160,165),…,第八组[190,195),得到频率分布直方图如图所示.
从某校高一年级1000名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米到195厘米之间,将测量结果分为八组:第一组[155,160),第二组[160,165),…,第八组[190,195),得到频率分布直方图如图所示.分析 (Ⅰ)由频率分布直方图分析可得各数据段的频率,再由频率与频数的关系,可得频数.
(Ⅱ)先求前四组的频率,进而可求中位数,计算可得各组频数,即可求解平均数.
解答 (本题满分为12分)
解:(Ⅰ)由第三组的频率为:[1-5×(0.008+0.008+0.012+0.016+0.016+0.06)]÷2=0.2,
则其样本数为:0.2×100=20,…3分
由5×(0.008+0.016)+0.2=0.32,
则该校高一年级1000名学生中身高在170厘米以下的人数约为:0.32×1000=320(人)…6分
(Ⅱ)前四组的频率为:5×(0.008+0.016)+0.4=0.52,0.52-0.5=0.02,
则中位数在第四组中,由$\frac{0.02}{0.2}$=0.1,可得:175-0.1×5=174.5,
所以中位数为174.5 cm,…9分
计算可得各组频数分别为:4,8,20,20,30,8,6,4,
平均数约为:(157.5×4+162.5×8+167.5×20+172.5×20+177.5×30+182.5×8+187.5×6+192.5×4)÷100=174.1(cm)…12分
点评 本题考查了频率分布直方图的应用,关键是正确分析频率分布直方图的数据信息,准确计算,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②④ | B. | ②③ | C. | ①④ | D. | ①③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图:Rt△ABC中,∠CAB=90°,AB=2,AC=$\frac{\sqrt{2}}{2}$,曲线E过C点,动点P在E上运动,且保持|PA|+|PB|的值不变.
如图:Rt△ABC中,∠CAB=90°,AB=2,AC=$\frac{\sqrt{2}}{2}$,曲线E过C点,动点P在E上运动,且保持|PA|+|PB|的值不变.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.125 | B. | 0.8 | C. | 1 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com