
【题目】已知全集U=R,集合A={x∈R|2x﹣3≥0},B={x|1<x<2},C={x∈N|1≤x<a}.
(Ⅰ)求A∪B;
(Ⅱ)若C中恰有五个元素,求整数a的值;
(Ⅲ)若A∩C=,求实数a的取值范围.
【答案】解:(Ⅰ)集合A={x∈R|2x﹣3≥0}=[ ![]() ,+∞),B={x|1<x<2}=(1,2),
,+∞),B={x|1<x<2}=(1,2),
∴A∪B=(1,+∞),
(Ⅱ)∵C={x∈N|1≤x<a},C中恰有五个元素,则整数a的值为6,
(Ⅲ)∵C={x∈N|1≤x<a}=[1,a),A∩C=,
∴1≤a≤2
【解析】(1)根据题意解出集合A、B,使用并集运算即可,(2)根据恰有五个元素可得出a的整数值为6,(3)解出集合C,由A∩C=可得到a的取值范围.
【考点精析】解答此题的关键在于理解交、并、补集的混合运算的相关知识,掌握求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某网店经营的一种商品进价是每件10元,根据一周的销售数据得出周销量P(件)与单价x(元)之间的关系如图折线所示,该网店与这种商品有关的周开支均为25元.
(I)根据周销量图写出周销量P(件)与单价x(元)之间的函数关系式;
(Ⅱ)写出周利润y(元)与单价x(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.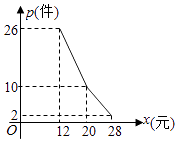
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知对数函数f(x)=logax(a>0,且a≠1)的图象经过点(4,2).
(1)求实数a的值;
(2)如果f(x+1)<0,求实数x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点A,B分别是椭圆 ![]() 的长轴的左右端点,点F为椭圆的右焦点,直线PF的方程为:
的长轴的左右端点,点F为椭圆的右焦点,直线PF的方程为: ![]() 且PA⊥PF.
且PA⊥PF. 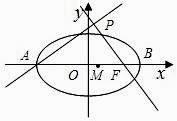
(1)求直线AP的方程;
(2)设点M是椭圆长轴AB上一点,点M到直线AP的距离等于|MB|,求椭圆上的点到点M的距离d的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的首项a1=1,前n项和为Sn , 且S1 , ![]() 成等差数列.
成等差数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}为递增的等比数列,且集合{b1 , b2 , b3}{a1 , a2 , a3 , a4 , a5},设数列{anbn}的前n项和为Tn , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱ABC﹣A1B1C1 中,AA1=AB=AC=1,E,F分别是CC1、BC 的中点,AE⊥ A1B1 , D为棱A1B1上的点.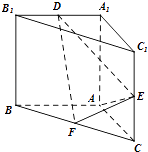
(1)证明:DF⊥AE;
(2)是否存在一点D,使得平面DEF与平面ABC所成锐二面角的余弦值为 ![]() ?若存在,说明点D的位置,若不存在,说明理由.
?若存在,说明点D的位置,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列所给4个图像中,与所给3件事吻合最好的顺序为( )
(1.)小明离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
(2.)小明骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
(3.)小明出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.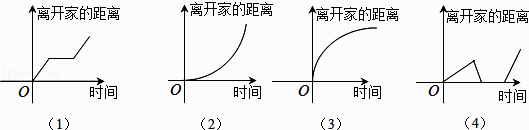
A.(4)(1)(2)
B.(4)(2)(3)
C.(4)(1)(3)
D.(1)(2)(4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com