
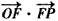 =1,
=1,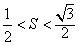 ,求向量
,求向量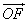 与
与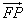 的夹角θ的取值范围;
的夹角θ的取值范围;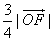 且
且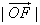 ≥2,当
≥2,当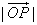 取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程。
取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程。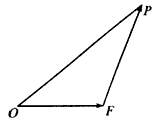
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:
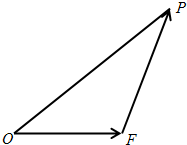 如图,设△OEP的面积为S,已知
如图,设△OEP的面积为S,已知| OF |
| FP |
| 1 |
| 2 |
| ||
| 2 |
| OF |
| FP |
| 3 |
| 4 |
| OF |
| OF |
| OP |
查看答案和解析>>
科目:高中数学 来源:宁夏银川一中2010届高三第四次月考、理科数学试卷 题型:044
如图,设△OFP的面积为S,已知![]() =1.
=1.
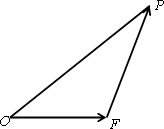
(1)若![]() <S<
<S<![]() ,求向量
,求向量![]() 与
与![]() 的夹角
的夹角![]() 的取值范围;
的取值范围;
(2)若S=![]() ,且
,且![]() ≥2,当
≥2,当![]() 取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程.
取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年云南省曲靖市宣威市飞翔高级中学高三(下)3月月考数学试卷(理科)(解析版) 题型:解答题
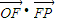 =1.
=1.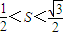 ,求向量
,求向量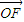 与
与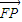 的夹角θ的取值范围;
的夹角θ的取值范围; |
|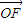 |,且|
|,且|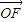 |≥2,当|
|≥2,当|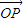 |取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程.
|取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程.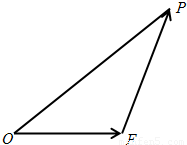
查看答案和解析>>
科目:高中数学 来源:2011年广东省高考数学第三轮复习精编模拟试卷12(理科)(解析版) 题型:解答题
 =1.
=1. ,求向量
,求向量 与
与 的夹角θ的取值范围;
的夹角θ的取值范围; |
| |,且|
|,且| |≥2,当|
|≥2,当| |取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程.
|取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com