
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若函数 ![]() 的图象在点
的图象在点 ![]() 处的切线的倾斜角为
处的切线的倾斜角为 ![]() ,对于任意的
,对于任意的![]() ,函数
,函数![]() 在区间
在区间![]() 上总不是单调函数, 求
上总不是单调函数, 求![]() 的取值范围;
的取值范围;
(3)求证:![]() .
.
【答案】(1)当![]() 时,单调增区间为
时,单调增区间为![]() ,减区间为
,减区间为![]() ,当
,当![]() 时,单调增区间为
时,单调增区间为![]() ,减区间为
,减区间为![]() ,当
,当![]() 时,
时,![]() 不是单调函数;(2)
不是单调函数;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
试题分析:(1)由![]() ,然后对
,然后对![]() 、
、 ![]() 和
和 ![]() 分三种情况进行讨论;(2)由题知可得
分三种情况进行讨论;(2)由题知可得![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 一定有两个不等的实根
一定有两个不等的实根![]() ,不妨设
,不妨设![]()
![]() 在
在![]() 上递减, 在
上递减, 在![]() 上递增
上递增![]()
![]()
![]()
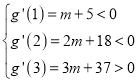
![]()
![]() ;(3)由(1)知当
;(3)由(1)知当![]() 时,
时,![]() 在
在![]() 上递增
上递增![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
试题解析:(1)由![]() ,①当
,①当![]() 时,显然
时,显然 ![]() 时,
时,![]() ;当
;当![]() 时,
时, ![]() ,所以此时
,所以此时![]() 的单调增区间为
的单调增区间为![]() 减区间为
减区间为![]() ; ②同理当
; ②同理当![]() 时,
时,![]() 的单调增区间为
的单调增区间为![]() , 减区间为
, 减区间为![]() ; ③当
; ③当 ![]() 时,
时,![]() 不是单调函数.
不是单调函数.
(2)由题知![]() ,得
,得![]() ,所以
,所以![]() ,所以
,所以![]() .因为
.因为![]() ,所以
,所以![]() 一定有两个不等的实根
一定有两个不等的实根![]() ,又因为
,又因为![]() .不妨设
.不妨设![]() , 由已知
, 由已知![]() 时
时![]() 时
时![]() ,即
,即![]() 在
在![]() 上递减, 在
上递减, 在![]() 上递增, 依题意知
上递增, 依题意知![]() ,于是只需
,于是只需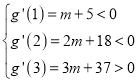 得
得![]() .
.
(3)由(1)知当![]() 时,
时, ![]() 在
在![]() 上递增, 所以
上递增, 所以 ![]() .在上式中分别令
.在上式中分别令![]() 得
得
![]() ,以上不等式相乘得
,以上不等式相乘得![]() ,两边同除以
,两边同除以![]() 得
得
![]() ,即证.
,即证.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】心理学家分析发现“喜欢空间想象”与“性别”有关,某数学兴趣小组为了验证此结论,从全体组员中按分层抽样的方法抽取50名同学(男生30人、女生20人),给每位同学立体几何题、代数题各一道,让各位同学自由选择一道题进行解答,选题情况统计如下表:(单位:人)
立体几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
(1)能否有97.5%以上的把握认为“喜欢空间想象”与“性别”有关?
(2)经统计得,选择做立体几何题的学生正答率为![]() ,且答对的学生中男生人数是女生人数的5倍,现从选择做立体几何题且答错的学生中任意抽取两人对他们的答题情况进行研究,求恰好抽到男女生各一人的概率.
,且答对的学生中男生人数是女生人数的5倍,现从选择做立体几何题且答错的学生中任意抽取两人对他们的答题情况进行研究,求恰好抽到男女生各一人的概率.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电脑公司在甲、乙两地各有一个分公司,甲分公司现有电脑6台,乙分公司现有同一型号的电脑12台.现A地某单位向该公司购买该型号的电脑10台,B地某单位向该公司购买该型号的电脑8台.已知从甲地运往A,B两地每台电脑的运费分别是40元和30元,从乙地运往A,B两地每台电脑的运费分别是80元和50元. 若总运费不超过1000元,则调运方案的种数为
A.1 B.2
C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医药研究所开发的一种药,如果成年人按规定的剂量服用,据监测,服药后每毫升中的含药量![]() (微克)与时间
(微克)与时间![]() (小时)之间近似满足如图所示的曲线.(当
(小时)之间近似满足如图所示的曲线.(当![]() 时,
时, ![]() ).
).
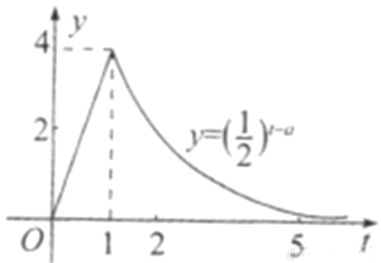
(1)写出第一次服药后![]() 与
与![]() 之间的函数关系式
之间的函数关系式![]() ;
;
(2)据进一步测定,每毫升血液中含药量不少于![]() 微克时,治疗疾病有效,求服药一次后治疗疾病有效时间.
微克时,治疗疾病有效,求服药一次后治疗疾病有效时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,几何体是圆柱的一部分,它是由矩形![]() (及其内部)以
(及其内部)以![]() 边所在直线为旋转轴旋转
边所在直线为旋转轴旋转![]() 得到的,
得到的, ![]() 是
是![]() 的中点.
的中点.
(![]() )设
)设![]() 是
是![]() 上的一点,且
上的一点,且![]() ,求
,求![]() 的大小;
的大小;
(![]() )当
)当![]() 时,求二面角
时,求二面角![]() 的大小.
的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=60°。
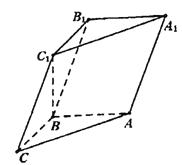
(Ⅰ)求证:C1B⊥平面ABC;
(Ⅱ)设![]() (0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,试求λ的值.
(0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,试求λ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com