
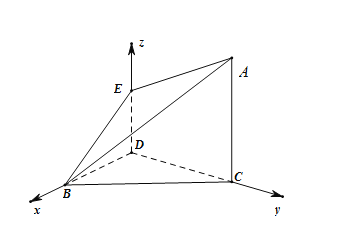
【题目】在如图所示的几何体中,![]() 平面
平面![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成二面角的正弦值.
所成二面角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】分析:(1)在![]() 中,由勾股定理可得
中,由勾股定理可得![]() .又
.又![]() 平面
平面![]() ,据此可得
,据此可得![]() .利用线面垂直的判断定理可得
.利用线面垂直的判断定理可得![]() 平面
平面![]() .
.
(2)(方法一)延长![]() ,
,![]() 相交于
相交于![]() ,连接
,连接![]() ,由题意可知二面角
,由题意可知二面角![]() 就是平面
就是平面![]() 与平面
与平面![]() 所成二面角.取
所成二面角.取![]() 的中点为
的中点为![]() ,则
,则![]() 就是二面角
就是二面角![]() 的平面角.结合几何关系计算可得
的平面角.结合几何关系计算可得![]() .
.
(方法二)建立空间直角坐标系![]() ,计算可得平面
,计算可得平面![]() 的法向量
的法向量![]() .取平面
.取平面![]() 的法向量为
的法向量为![]() .利用空间向量计算可得
.利用空间向量计算可得![]() .
.
详解:(1)在![]() 中,
中,![]() .
.
所以![]() ,所以
,所以![]() 为直角三角形,
为直角三角形,![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
而![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)(方法一)如图延长![]() ,
,![]() 相交于
相交于![]() ,连接
,连接![]() ,
,
则平面![]() 平面
平面![]() .
.
二面角![]() 就是平面
就是平面![]() 与平面
与平面![]() 所成二面角.
所成二面角.
因为![]() ,所以
,所以![]() 是
是![]() 的中位线.
的中位线.
![]() ,这样
,这样![]() 是等边三角形.
是等边三角形.
取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,因为
,因为![]() 平面
平面![]() .
.
所以![]() 就是二面角
就是二面角![]() 的平面角.
的平面角.
在![]() ,所以
,所以![]() .
.

(方法二)建立如图所示的空间直角坐标系![]() ,可得
,可得![]() .
.
![]() .
.
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则
令![]() 得
得![]() .
.
取平面![]() 的法向量为
的法向量为![]() .
.
设平面![]() 与平面
与平面![]() 所成二面角的平面角为
所成二面角的平面角为![]() ,
,
则 ,从而
,从而![]() .
.


科目:高中数学 来源: 题型:
【题目】国家放开计划生育政策,鼓励一对夫妇生育2个孩子.在某地区的100000对已经生育了一胎夫妇中,进行大数据统计得,有100对第一胎生育的是双胞胎或多胞胎,其余的均为单胞胎.在这99900对恰好生育一孩的夫妇中,男方、女方都愿意生育二孩的有50000对,男方愿意生育二孩女方不愿意生育二孩的有![]() 对,男方不愿意生育二孩女方愿意生育二孩的有
对,男方不愿意生育二孩女方愿意生育二孩的有![]() 对,其余情形有
对,其余情形有![]() 对,且
对,且![]() .现用样本的频率来估计总体的概率.
.现用样本的频率来估计总体的概率.
(1)说明“其余情形”指何种具体情形,并求出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)该地区为进一步鼓励生育二孩,实行贴补政策:凡第一胎生育了一孩的夫妇一次性贴补5000元,第一胎生育了双胞胎或多胞胎的夫妇只有一次性贴补15000元.第一胎已经生育了一孩再生育了二孩的夫妇一次性再贴补20000元.这种补贴政策直接提高了夫妇生育二孩的积极性:原先男方或女方中只有一方愿意生育二孩的夫妇现在都愿意生育二孩,但原先男方、女方都不愿意生育二孩的夫妇仍然不愿意生育二孩.设![]() 为该地区的一对夫妇享受的生育贴补,求
为该地区的一对夫妇享受的生育贴补,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年2月22日,在韩国平昌冬奥会短道速滑男子500米比赛中,中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造中国男子冰上竞速项目在冬奥会金牌零的突破.根据短道速滑男子500米的比赛规则,运动员自出发点出发进入滑行阶段后,每滑行一圈都要经过4个直道与弯道的交接口![]() .已知某男子速滑运动员顺利通过每个交接口的概率均为
.已知某男子速滑运动员顺利通过每个交接口的概率均为![]() ,摔倒的概率均为
,摔倒的概率均为![]() .假定运动员只有在摔倒或达到终点时才停止滑行,现在用
.假定运动员只有在摔倒或达到终点时才停止滑行,现在用![]() 表示该运动员在滑行最后一圈时在这一圈后已经顺利通过的交接口数.
表示该运动员在滑行最后一圈时在这一圈后已经顺利通过的交接口数.

(1)求该运动员停止滑行时恰好已顺利通过3个交接口的概率;
(2)求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某商品在过去20天的日销售量和日销售价格均为销售时间t(天)的函数,日销售量(单位:件)近似地满足: ![]() ,日销售价格(单位:元)近似地满
,日销售价格(单位:元)近似地满
足: ![]()
(I)写出该商品的日销售额S关于时间t的函数关系;
(Ⅱ)当t等于多少时,日销售额S最大?并求出最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 有两个不同零点
有两个不同零点![]() .设函数
.设函数![]() 的定义域为
的定义域为![]() ,且
,且![]() 的最大值记为
的最大值记为![]() ,最小值记为
,最小值记为![]() .
.
(1)求![]() (用
(用![]() 表示);
表示);
(2)当![]() 时,试问以
时,试问以![]() 为长度的线段能否构成一个三角形,如果不一定,进一步求出
为长度的线段能否构成一个三角形,如果不一定,进一步求出![]() 的取值范围,使它们能构成一个三角形;
的取值范围,使它们能构成一个三角形;
(3)求![]() 和
和![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com