
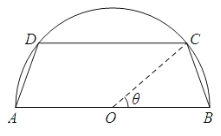
【题目】一个圆柱形圆木的底面半径为1 m,长为10 m,将此圆木沿轴所在的平面剖成两部分.现要把其中一部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD(如图所示,其中O为圆心,C,D在半圆上),设![]() ,木梁的体积为V(单位:m3),表面积为S(单位:m2).
,木梁的体积为V(单位:m3),表面积为S(单位:m2).
(1)求V关于θ的函数表达式;
(2)求![]() 的值,使体积V最大;
的值,使体积V最大;
(3)问当木梁的体积V最大时,其表面积S是否也最大?请说明理由.
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0),直线l与抛物线C相交于A,B两点,P为抛物线上一点,当直线l过抛物线焦点时,|AB|的最小值为2.
(Ⅰ)求抛物线C的方程;
(Ⅱ)若AB的中点为(3,1),且直线PA,PB的倾斜角互补,求△PAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有甲、乙两个研发小组,他们研发新产品成功的概率分别为 ![]() 和
和 ![]() .现安排甲组研发新产品A,乙组研发新产品B,设甲、乙两组的研发相互独立.
.现安排甲组研发新产品A,乙组研发新产品B,设甲、乙两组的研发相互独立.
(Ⅰ)求至少有一种新产品研发成功的概率;
(Ⅱ)若新产品A研发成功,预计企业可获利润120万元;若新产品B研发成功,预计企业可获利润100万元,求该企业可获利润的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图.
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() .
.
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤.
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=aln(x﹣1),g(x)=x2+bx,F(x)=f(x+1)﹣g(x),其中a,b∈R.
(1)若y=f(x)与y=g(x)的图象在交点(2,k)处的切线互相垂直,求a,b的值;
(2)若x=2是函数F(x)的一个极值点,x0和1是F(x)的两个零点,且x0∈(n,n+1)n∈N,求n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log4(4x+1)+kx与g(x)=log4(a2x﹣![]() a),其中f(x)是偶函数.
a),其中f(x)是偶函数.
(1)求实数k的值;
(2)求函数g(x)的定义域;
(3)若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com