
设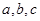 均为正数,且
均为正数,且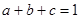
证明:(1)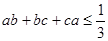 ;
;
(2)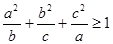 .
.
科目:高中数学 来源: 题型:
 选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
|
|
|
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
查看答案和解析>>
科目:高中数学 来源:江苏省苏泰州南通2010届高三第三次模拟考试 题型:解答题
(选做题)本大题包括A,B,C,D共4小题,请从这4题中选做2小题. 每小题10分,共20分.请在答题卡上准确填涂题目标记. 解答时应写出文字说明、证明过程或演算步骤.
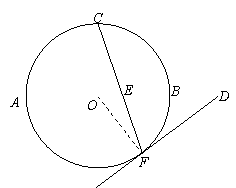 A. 选修4-1:几何证明选讲
A. 选修4-1:几何证明选讲
如图,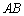 是⊙
是⊙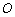 的直径,
的直径,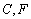 是⊙
是⊙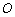 上的两点,
上的两点,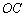 ⊥
⊥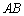 ,
,
过点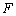 作⊙
作⊙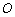 的切线FD交
的切线FD交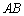 的延长线于点
的延长线于点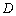 .连结
.连结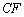 交
交
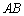 于点
于点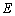 .
.
求证: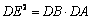 .
.
B. 选修4-2:矩阵与变换
求矩阵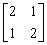 的特征值及对应的特征向量.
的特征值及对应的特征向量.
C. 选修4-4:坐标系与参数方程
已知曲线 的极坐标方程是
的极坐标方程是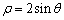 ,直线
,直线 的参数方程是
的参数方程是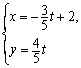 (
(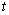 为参数).
为参数).
(1)将曲线 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)设直线 与
与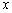 轴的交点是
轴的交点是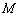 ,
,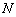 是曲线
是曲线 上一动点,求
上一动点,求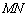 的最大值.
的最大值.
D.选修4-5:不等式选讲
设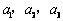 均为正数,且
均为正数,且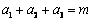 ,求证
,求证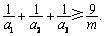
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com