
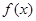 是定义在
是定义在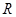 上的奇函数,当
上的奇函数,当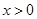 时的解析式为
时的解析式为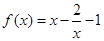 .
.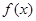 的解析式;
的解析式;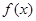 的零点.
的零点. 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源:不详 题型:解答题
 是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛
是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛 扩建成一个更大的矩形花园
扩建成一个更大的矩形花园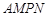 ,要求:B在
,要求:B在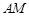 上,D在
上,D在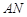 上,对角线
上,对角线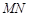 过C点,且矩形
过C点,且矩形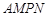 的面积小于64平方米.
的面积小于64平方米.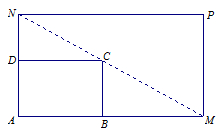
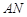 长为
长为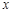 米,矩形
米,矩形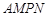 的面积为
的面积为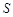 平方米,试用解析式将
平方米,试用解析式将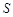 表示成
表示成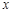 的函数,并写出该函数的定义域;
的函数,并写出该函数的定义域;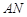 的长度是多少时,矩形
的长度是多少时,矩形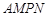 的面积最小?并求最小面积.
的面积最小?并求最小面积.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
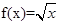 (0<x≤1),求x∈[-5,-4]时,函数f(x)的解析式.
(0<x≤1),求x∈[-5,-4]时,函数f(x)的解析式.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
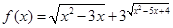 的最小值是3
的最小值是3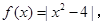 若
若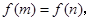 且
且 ,则动点
,则动点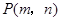 到直线
到直线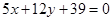 的
的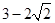 .
.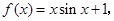 当
当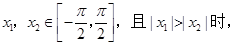
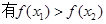 ”是真命题.
”是真命题.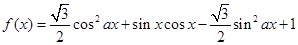 的最小正周期是1的充要条件是
的最小正周期是1的充要条件是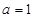 .
.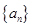 的前
的前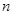 项和为
项和为 ,
,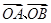 为不共线的向量,又
为不共线的向量,又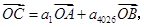
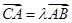 ,则
,则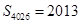 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
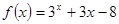 ,用二分法求方程
,用二分法求方程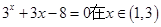 内近似解的过程中,取区间中点
内近似解的过程中,取区间中点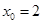 ,那么下一个有根区间为 ( )
,那么下一个有根区间为 ( )| A.(1,2) | B.(2,3) |
| C.(1,2)或(2,3)都可以 | D.不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com