
【题目】设直线![]() 分别是函数
分别是函数![]() 图象上点
图象上点![]() 处的切线,
处的切线,![]() 垂直相交于点
垂直相交于点![]() ,且
,且![]() 分别与
分别与![]() 轴相交于点A,B,则△PAB的面积的取值范围是( )
轴相交于点A,B,则△PAB的面积的取值范围是( )
A. (1,+∞) B. (0,2) C. (0,+∞) D. (0,1)
【答案】D
【解析】
设出点P1,P2的坐标,求出原分段函数的导函数,得到直线l1与l2的斜率,由两直线垂直求得P1,P2的横坐标的乘积为1,再分别写出两直线的点斜式方程,求得A,B两点的纵坐标,得到|AB|,联立两直线方程求得P的横坐标,然后代入三角形面积公式,利用基本不等式求得△PAB的面积的取值范围.
解:设P1(x1,y1),P2(x2,y2)(0<x1<1<x2),
当0<x<1时,f′(x)![]() ,当x>1时,f′(x)
,当x>1时,f′(x)![]() ,
,
∴l1的斜率![]() ,l2的斜率
,l2的斜率![]() ,
,
∵l1与l2垂直,且x2>x1>0,
∴![]() ,即x1x2=1.
,即x1x2=1.
直线l1:![]() ,l2:
,l2:![]() .
.
取x=0分别得到A(0,1﹣lnx1),B(0,﹣1+lnx2),
|AB|=|1﹣lnx1﹣(﹣1+lnx2)|=|2﹣(lnx1+lnx2)|=|2﹣lnx1x2|=2.
联立两直线方程可得交点P的横坐标为x![]() ,
,
∴![]() |AB||xP|
|AB||xP|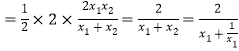 .
.
∵函数y=x![]() 在(0,1)上为减函数,且0<x1<1,
在(0,1)上为减函数,且0<x1<1,
∴![]() ,则
,则![]() ,
,
∴![]() .
.
∴△PAB的面积的取值范围是(0,1).
故选:D.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() .
.
⑴若![]() 的定义域为
的定义域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
⑵当![]() ,求函数
,求函数![]() 的最小值
的最小值![]() ;
;
⑶是否存在实数![]() ,使得函数
,使得函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() 上,
上, ![]() 为椭圆
为椭圆![]() 的右焦点,
的右焦点, ![]() 分别为椭圆
分别为椭圆![]() 的左,右两个顶点.若过点
的左,右两个顶点.若过点![]() 且斜率不为0的直线
且斜率不为0的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且线段
两点,且线段![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与
与![]() 相交于点
相交于点![]() ,证明:
,证明: ![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)一个盒子里装有三张卡片,分别标记有数字![]() ,
,![]() ,
,![]() ,这三张卡片除标记的数字外完全相同。随机有放回地抽取
,这三张卡片除标记的数字外完全相同。随机有放回地抽取![]() 次,每次抽取
次,每次抽取![]() 张,将抽取的卡片上的数字依次记为
张,将抽取的卡片上的数字依次记为![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求“抽取的卡片上的数字满足![]() ”的概率;
”的概率;
(Ⅱ)求“抽取的卡片上的数字![]() ,
,![]() ,
,![]() 不完全相同”的概率.
不完全相同”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店经营的某种消费品的进价为每件14元,月销售量![]() (百件)与每件的销售价格
(百件)与每件的销售价格![]() (元)的关系如图所示,每月各种开支2 000元.
(元)的关系如图所示,每月各种开支2 000元.

(1)写出月销售量![]() (百件)关于每件的销售价格
(百件)关于每件的销售价格![]() (元)的函数关系式.
(元)的函数关系式.
(2)写出月利润![]() (元)与每件的销售价格
(元)与每件的销售价格![]() (元)的函数关系式.
(元)的函数关系式.
(3)当该消费品每件的销售价格为多少元时,月利润最大?并求出最大月利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,
中,![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点.动直线
的左、右焦点.动直线![]() 过点
过点![]() ,且与椭圆
,且与椭圆![]() 相交于
相交于![]() ,
,![]() 两点(直线
两点(直线![]() 与
与![]() 轴不重合).
轴不重合).

(1)若点![]() 的坐标为
的坐标为![]() ,求点
,求点![]() 坐标;
坐标;
(2)点![]() ,设直线
,设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,求证:
,求证:![]() ;
;
(3)求![]() 面积最大时的直线
面积最大时的直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com