Question

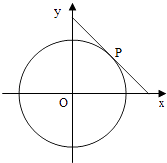
【题目】圆x2+y2=4的切线与x轴正半轴，y轴正半轴围成一个三角形，当该三角形面积最小时，切点为P（如图），双曲线C1： 过点P且离心率为 ．

（1）求C1的方程；
（2）若椭圆C2过点P且与C1有相同的焦点，直线l过C2的右焦点且与C2交于A，B两点，若以线段AB为直径的圆过点P，求l的方程．

Answer 1

【答案】
（1）解：设切点P（x0，y0），（x0＞0，y0＞0），则切线的斜率为 ，

可得切线的方程为 ，化为x0x+y0y=4．

令x=0，可得 ；令y=0，可得 ．

∴切线与x轴正半轴，y轴正半轴围成一个三角形的面积S= = ．

∵4= ，当且仅当 时取等号．

∴ ．此时P ．

由题意可得 ， ，解得a2=1，b2=2．

故双曲线C1的方程为 ．

（2）解：由（1）可知双曲线C1的焦点（± ，0），即为椭圆C2的焦点．

可设椭圆C2的方程为 （b1＞0）．

把P 代入可得 ，解得 =3，

因此椭圆C2的方程为 ．

由题意可设直线l的方程为x=my+ ，A（x1，y1），B（x2，y2），

联立 ，化为 ，

∴ ， ．

∴x1+x2= = ，

x1x2= = ．

， ，

∵ ，∴ ，

∴ + ，

∴ ，解得m= -1或m= ，

因此直线l的方程为： 或

【解析】（1）设切点P（x0 ， y0），（x0＞0，y0＞0），利用相互垂直的直线斜率之间的关系可得切线的斜率和切线的方程，即可得出三角形的面积，利用基本不等式的性质可得点P的坐标，再利用双曲线的标准方程及其性质即可得出；（2）由（1）可得椭圆C2的焦点．可设椭圆C2的方程为 （b1＞0）．把P的坐标代入即可得出方程．由题意可设直线l的方程为x=my+ ，A（x1 ， y1），B（x2 ， y2），与椭圆的方程联立即可得出根与系数的关系，再利用向量垂直与数量积的关系即可得出．