
【题目】若分别为P(1,0)、Q(2,0),R(4,0)、S(8,0)四个点各作一条直线,所得四条直线恰围成正方形,则该正方形的面积不可能为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:如果过点P(1,0),Q(2,0),R(4,0),S(8,0)作四条直线构成一个正方形, 过P点的必须和过Q,R,S的其中一条直线平行和另外两条垂直,
假设过P点和Q点的直线相互平行时,如图,
设直线PC与x轴正方向的夹角为θ,再过Q作它的平行线QD,过R、S作它们的垂线RB、SC,过点A作x轴的平行线分别角PC、SC于点M、N,
则AB=AMsinθ=PQsinθ=sinθ,AD=ANcosθ=RScosθ=4cosθ,
因为AB=AD,所以sinθ=4cosθ,则tanθ=4,
所以正方形ABCD的面积S=ABAD=4sinθcosθ= ![]() =
= ![]() =
= ![]() ,
,
同理可求,当直线PC和过R的直线平行时正方形ABCD的面积S为 ![]() ,
,
当直线PC和过S点的直线平行时正方形ABCD的面积S为 ![]() ,
,
故选:C.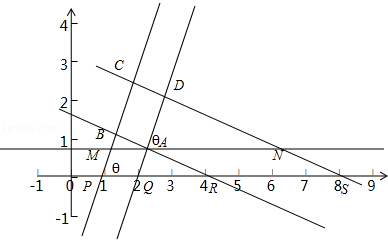
【考点精析】解答此题的关键在于理解两点式方程的相关知识,掌握直线的两点式方程:已知两点![]() 其中
其中![]() 则:y-y1/y-y2=x-x1/x-x2.
则:y-y1/y-y2=x-x1/x-x2.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的半焦距为
的半焦距为 ![]() ,原点
,原点 ![]() 到经过两点
到经过两点 ![]() 的直线的距离为
的直线的距离为 ![]() .
.
(Ⅰ)求椭圆 ![]() 的离心率;
的离心率;
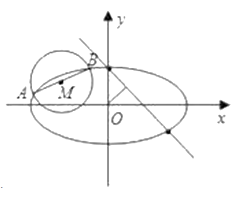
(Ⅱ)如图, ![]() 是圆
是圆 ![]() 的一条直径,若椭圆
的一条直径,若椭圆 ![]() 经过
经过 ![]() 两点,求椭圆
两点,求椭圆 ![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在实数集R上的奇函数f(x)有最小正周期2,且当x∈(0,1)时, ![]() .
.
(Ⅰ)求函数f(x)在(-1,1)上的解析式;
(Ⅱ)判断f(x)在(0,1)上的单调性;
(Ⅲ)当λ取何值时,方程f(x)=λ在(-1,1)上有实数解?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正四面体P﹣ABC中,点M是棱PC的中点,点N是线段AB上一动点,且 ![]() ,设异面直线 NM 与 AC 所成角为α,当
,设异面直线 NM 与 AC 所成角为α,当 ![]() 时,则cosα的取值范围是 .
时,则cosα的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点P在△ABC的BC边所在的直线上从左到右运动,设△ABP与△ACP的外接圆面积之比为λ,当点P不与B,C重合时,( )
A.λ先变小再变大
B.当M为线段BC中点时,λ最大
C.λ先变大再变小
D.λ是一个定值
查看答案和解析>>
科目:高中数学 来源: 题型:
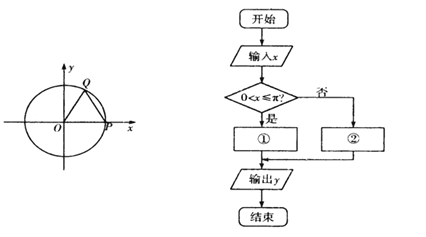
【题目】如图,已知单位圆x2+y2=1与x轴正半轴交于点P,当圆上一动点Q从P出发沿逆时针方向旋转一周回到P点后停止运动设OQ扫过的扇形对应的圆心角为xrad,当0<x<2π时,设圆心O到直线PQ的距离为y,y与x的函数关系式y=f(x)是如图所示的程序框图中的①②两个关系式
(Ⅰ)写出程序框图中①②处的函数关系式;
(Ⅱ)若输出的y值为2,求点Q的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+ ![]() ,a∈R.
,a∈R.
(1)若f(x)的最小值为0,求实数a的值;
(2)证明:当a=2时,不等式f(x)≥ ![]() ﹣e1﹣x恒成立.
﹣e1﹣x恒成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com