
【题目】袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为![]() .现有甲、乙两人从袋中轮流、不放回地摸取1球,甲先取,乙后取,然后甲再取……直到袋中的球取完即终止.若摸出白球,则记2分,若摸出黑球,则记1分.每个球在每一次被取出的机会是等可能的.
.现有甲、乙两人从袋中轮流、不放回地摸取1球,甲先取,乙后取,然后甲再取……直到袋中的球取完即终止.若摸出白球,则记2分,若摸出黑球,则记1分.每个球在每一次被取出的机会是等可能的.
(1)求袋中白球的个数;
(2)用表示甲,乙最终得分差的绝对值,求随机变量![]() 的概率分布列及数学期望E
的概率分布列及数学期望E![]() .
.
【答案】(1)3;
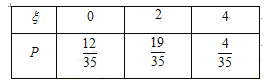
(2)x的概率分布列为:
![]() .
.
【解析】
试题(1)这属于古典概型问题,从7个球中任取两个,共有![]() 种取法,而如果其中有
种取法,而如果其中有![]() 个白球,则任取两个白球的取法为
个白球,则任取两个白球的取法为![]() ,由题意有
,由题意有![]() ,解之得
,解之得![]() ;(2)首先要知道随机变量
;(2)首先要知道随机变量![]() 的所有可能取值,由(1)可知,袋中有3个白球、4个黑球,甲四次取球可能的情况是:4个黑球、3黑1白、2黑2白、1黑3白.相应的分数之和为4分、5分、6分、7分;与之对应的乙取球情况:3个白球、1黑2白、2黑1白、3黑,相应分数之和为6分、5分、4分、3分;即x可能的取值是0,2,4.,再利用公式计算可得分布列和期望.
的所有可能取值,由(1)可知,袋中有3个白球、4个黑球,甲四次取球可能的情况是:4个黑球、3黑1白、2黑2白、1黑3白.相应的分数之和为4分、5分、6分、7分;与之对应的乙取球情况:3个白球、1黑2白、2黑1白、3黑,相应分数之和为6分、5分、4分、3分;即x可能的取值是0,2,4.,再利用公式计算可得分布列和期望.
试题解析:(1)设袋中原有n个白球,由题意,知![]() ,
,
解之得n=3或n=-2(舍去),即袋中原有3个白球;
(2)由(1)可知,袋中有3个白球、4个黑球.甲四次取球可能的情况是:4个黑球、3黑1白、2黑2白、1黑3白.相应的分数之和为4分、5分、6分、7分;与之对应的乙取球情况:3个白球、1黑2白、2黑1白、3黑,相应分数之和为6分、5分、4分、3分;即x可能的取值是0,2,4.
![]() ;
;
![]() ;
;![]() ,
,
所以x的概率分布列为:

![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,曲线y=f(x)在点(1,f(1))处的切线方程为y=x.
,曲线y=f(x)在点(1,f(1))处的切线方程为y=x.
(1)求函数f(x)的单调区间及极值;
(2)若x≥1,f(x)≤kx恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由0,1,2,3,4,5,6,7,8,9组成没有重复数字的五位数,且是奇数,其中恰有两个数字是偶数,则这样的五位数的个数为( ).
A.7200B.6480C.4320D.5040
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高三理科班共有![]() 名同学参加某次考试,从中随机挑出
名同学参加某次考试,从中随机挑出![]() 名同学,他们的数学成绩
名同学,他们的数学成绩![]() 与物理成绩
与物理成绩![]() 如下表:
如下表:
数学成绩 |
|
|
|
|
|
物理成绩 |
|
|
|
|
|
(1)数据表明![]() 与
与![]() 之间有较强的线性关系,求
之间有较强的线性关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)本次考试中,规定数学成绩达到![]() 分为优秀,物理成绩达到
分为优秀,物理成绩达到![]() 分为优秀.若该班数学优秀率与物理优秀率分别为
分为优秀.若该班数学优秀率与物理优秀率分别为![]() 和
和![]() ,且除去抽走的
,且除去抽走的![]() 名同学外,剩下的同学中数学优秀但物理不优秀的同学共有
名同学外,剩下的同学中数学优秀但物理不优秀的同学共有![]() 人,请写出
人,请写出![]() 列联表,判断能否在犯错误的概率不超过
列联表,判断能否在犯错误的概率不超过![]() 的前提下认为数学优秀与物理优秀有关?
的前提下认为数学优秀与物理优秀有关?
参考数据: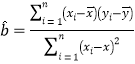 ,
,![]() ;
;![]() ,
,![]() ;
;![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某媒体对“男女延迟退休″这一公众关注的问题进行名意调查,如表是在某单位得到的数据:
赞同 | 反对 | 合计 | |
男 | 50 | 150 | 200 |
女 | 30 | 170 | 200 |
合计 | 80 | 320 | 400 |
(I)能否有97.5%的把握认为对这一问题的看法与性别有关?
(II)从赞同“男女延迟退休”的80人中,利用分层抽样的方法抽出8人,然后从中选出3人进行陈述发言,设发言的女士人数为X,求X的分布列和期望.
参考公式:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x)是定义在区间[-c,c]上的奇函数,其图象如下图所示.令g(x)=af(x)+b,则下列关于函数g(x)的结论:
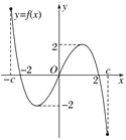
①若a<0,则函数g(x)的图象关于原点对称;
②若a=-1,-2<b<0,则方程g(x)=0有大于2的实根;
③若a≠0,b=2,则方程g(x)=0有两个实根;
④若a≠0,b=2,则方程g(x)=0有三个实根.
其中,正确的结论为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com