
【题目】设![]() :实数
:实数![]() 满足
满足![]() ,其中
,其中![]() ;
; ![]() :实数
:实数![]() 满足
满足![]() .
.
(1)若![]() ,且
,且![]() 为真,求实数
为真,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 是
是![]() 的必要不充分条件,求实数
的必要不充分条件,求实数![]() 的取值范围.
的取值范围.
【答案】(1) 实数![]() 的取值范围是
的取值范围是![]() ;(2) 实数
;(2) 实数![]() 的取值范围是
的取值范围是![]() .
.
【解析】试题分析:(1)利用一元二次不等式的解法可化简命题p,q,若p∨q为真,则p,q至少有1个为真,即可得出;(2)根据p是q的必要不充分条件,即可得出.
试题解析:
(1)由x2﹣4ax+3a2<0,得(x﹣3a)(x﹣a)<0,
又a>0,所以a<x<3a,
当a=1时,1<x<3,即p为真时实数x的取值范围是1<x<3.
q为真时![]() 等价于(x﹣2)(x﹣3)<0,得2<x<3,
等价于(x﹣2)(x﹣3)<0,得2<x<3,
即q为真时实数x的取值范围是2<x<3.
若p∨q为真,则实数x的取值范围是1<x<3.
(2)p是q的必要不充分条件,等价于qp且p推不出q,
设A={x|a<x<3a},B={x|2<x<3},则BA;
则 ,
,
所以实数a的取值范围是1≤a≤2。


科目:高中数学 来源: 题型:
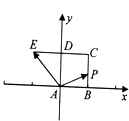
【题目】如图,已知正方形ABCD的边长为1,E在CD延长线上,且DE=CD.动点P从点A出发沿正方形ABCD的边按逆进针方向运动一周回到A点,其中 ![]() =λ
=λ ![]() +μ
+μ ![]() ,则下列命题正确的是 . (填上所有正确命题的序号)
,则下列命题正确的是 . (填上所有正确命题的序号)
①当点P为AD中点时,λ+μ=1;
②λ+μ的最大值为3;
③若y为给定的正数,则一存在向量 ![]() 和实数x,使
和实数x,使 ![]() =x
=x ![]() +y
+y ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(![]() 吨)与相应的生产能耗
吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
| 1 | 2 | 3 | 4 | 5 |
| 2 | 3 | 6 | 9 | 10 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)已知该厂技术改造前100吨甲产品能耗为200吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①三点确定一个平面;
②三条两两相交的直线确定一个平面;
③在空间上,与不共面四点A,B,C,D距离相等的平面恰有7个;
④两个相交平面把空间分成四个区域.
其中真命题的序号是 (写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域D,如果存在正实数m,使得对任意x∈D,都有f(x+m)>f(x),则称f(x)为D上的“m型增函数”.已知函数f(x)是定义在R上的奇函数,且当x>0时,f(x)=|x﹣a|﹣a(a∈R).若f(x)为R上的“20型增函数”,则实数a的取值范围是( )
A.a>0
B.a<5
C.a<10
D.a<20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com