


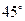 因为AE=CD=
因为AE=CD=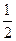 AB,所以BE=AE=CE
AB,所以BE=AE=CE 所以∠BCE==
所以∠BCE==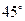 所以∠ACB=∠ACE+∠BCE=
所以∠ACB=∠ACE+∠BCE=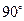
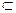
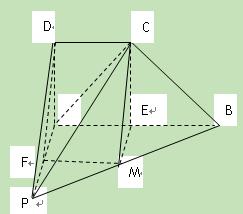
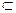 又因为BC⊥PC,AC∩PC="C,AC " 平面PAC,PC 平面 PAC
又因为BC⊥PC,AC∩PC="C,AC " 平面PAC,PC 平面 PAC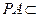 平面 PAC,所以PA⊥BC. ………………… 6分
平面 PAC,所以PA⊥BC. ………………… 6分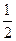 AB,因为CD∥AB,CD=
AB,因为CD∥AB,CD=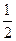 AB,所以FM∥CD,FM="CD. " ………9分
AB,所以FM∥CD,FM="CD. " ………9分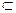 平面PAD ,CM
平面PAD ,CM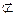 平面PAD,所以,CM∥平面PAD. ……………… 12分
平面PAD,所以,CM∥平面PAD. ……………… 12分 

科目:高中数学 来源:不详 题型:单选题
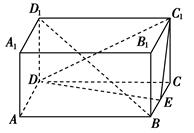
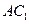 的棱长为,过点
的棱长为,过点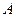 作平面
作平面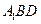 的垂线,垂足为点
的垂线,垂足为点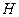 ,则以下命题中,错误的命题是( )
,则以下命题中,错误的命题是( )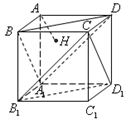
A.点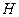 是 是 的垂心 的垂心 |
B.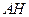 的延长线经过点 的延长线经过点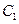 |
C.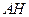 垂直平面 垂直平面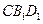 |
D.直线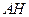 和 和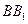 所成角为 所成角为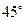 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
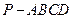 中,侧棱
中,侧棱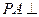 平面
平面 ,底面
,底面 是平行四边形,
是平行四边形,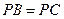 ,
,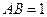 ,
,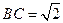 ,
,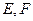 分别是
分别是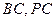 的中点.
的中点. 平面
平面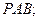
 与底面
与底面 所成二面角为
所成二面角为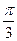 时,求二面角
时,求二面角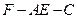 的大小.
的大小.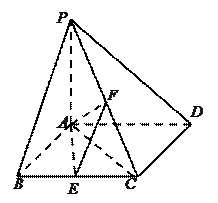
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
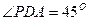 ,
, 求证:MN⊥平面PCD.
求证:MN⊥平面PCD.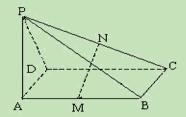
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
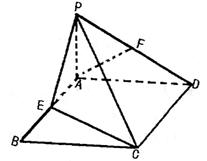
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com