

 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
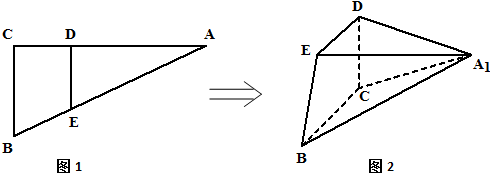
查看答案和解析>>
科目:高中数学 来源: 题型:
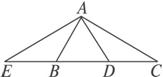
图1-9
A.△AED∽△ACB B.△AEB∽△ACD
C.△BAE∽△ACE D.△AEC∽△DAC
查看答案和解析>>
科目:高中数学 来源:2015届河南省分校高一上学期入学考试数学试卷(解析版) 题型:解答题
如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若点B,P在直线a的异侧,BM⊥直线a于点M.CN⊥直线a于点N,连接PM,PN.
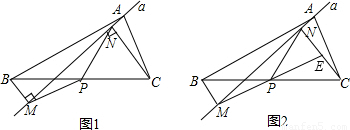
(1)延长MP交CN于点E(如图2).
①求证:△BPM≌△CPE;
②求证:PM=PN;
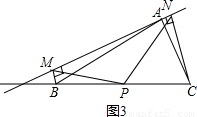
(2)若直线a绕点A旋转到图3的位置时,点B,P在直线a的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;
(3)若直线a绕点A旋转到与BC边平行的位置时,其它条件不变,请直接判断四边形MBCN的形状及此时PM=PN还成立吗?不必说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com