
【题目】北方某市一次全市高中女生身高统计调查数据显示:全市20000名高中女生的身高(单位:![]() )服从正态分布
)服从正态分布![]() .现从某高中女生中随机抽取50名测量身高,测量发现被测学生身高全部在
.现从某高中女生中随机抽取50名测量身高,测量发现被测学生身高全部在![]() 和
和![]() 之间,现将测量结果按如下方式分成6组:第1组
之间,现将测量结果按如下方式分成6组:第1组![]() ,第2组
,第2组![]() ,…,第6组
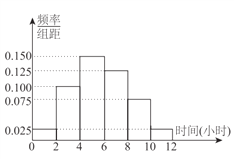
,…,第6组![]() ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.

(1)求这50名女生身高不低于172![]() 的人数;
的人数;
(2)在这50名女生身高不低于172![]() 的人中任意抽取2人,将该2人中身高排名(从高到低)在全市前260名的人数记为
的人中任意抽取2人,将该2人中身高排名(从高到低)在全市前260名的人数记为![]() ,求
,求![]() 的数学期望.
的数学期望.
参数数据:![]() ,
,
![]() .
.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设![]() 是平面直角坐标系中两两不同的四点,若
是平面直角坐标系中两两不同的四点,若![]() ,
,![]() ,且
,且![]() ,则称
,则称![]() 调和分割
调和分割![]() .已知平面上的点
.已知平面上的点![]() 调和分割点
调和分割点![]() ,则下列说法正确的是
,则下列说法正确的是
A. ![]() 可能线段
可能线段![]() 的中点
的中点
B. ![]() 可能线段
可能线段![]() 的中点
的中点
C. ![]() 可能同时在线段
可能同时在线段![]() 上
上
D. ![]() 不可能同时在线段
不可能同时在线段![]() 的延长线上
的延长线上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了提高学生的身体素质,决定组建学校足球队,学校为了解学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12.
(1)求该校报名学生的总人数;
(2)从报名的学生中任选3人,设X表示体重超过60kg的学生人数,求X的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,b>0,函数f(x)=x2+(ab﹣a﹣4b)x+ab是偶函数,则f(x)的图象与y轴交点纵坐标的最小值为( )
A.16
B.8
C.4
D.2![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学共有5000人,其中男生3500人,女生1500人,为了了解该校学生每周平均体育锻炼时间的情况以及该校学生每周平均体育锻炼时间是否与性别有关,现在用分层抽样的方法从中收集300位学生每周平均体育锻炼时间的样本数据(单位:小时),其频率分布直方图如下:
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
已知在样本数据中,有60位女生的每周平均体育锻炼时间超过4小时,根据独立性检验原理,我们( )
A. 没有理由认为“该校学生每周平均体育锻炼时间与性别有关”
B. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别有关”
的把握认为“该校学生每周平均体育锻炼时间与性别有关”
C. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别无关”
的把握认为“该校学生每周平均体育锻炼时间与性别无关”
D. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别有关”
的把握认为“该校学生每周平均体育锻炼时间与性别有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex·(a+![]() +lnx),其中a∈R.
+lnx),其中a∈R.
(I)若曲线y=f(x)在x=1处的切线与直线y=-![]() 垂直,求a的值;
垂直,求a的值;
(II)当a∈(0,ln2)时,证明:f(x)存在极小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,则下列说法正确的是( ).
的图象,则下列说法正确的是( ).
A. ![]() B. 直线
B. 直线![]() 是
是![]() 的图象的一条对称轴
的图象的一条对称轴
C. ![]() 的最小正周期为
的最小正周期为![]() D.
D. ![]() 为奇函数
为奇函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com