
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程
的参数方程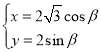 (
(![]() 为参数).直线
为参数).直线![]() 的参数方程
的参数方程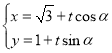 (
(![]() 为参数).
为参数).
(Ⅰ)求曲线![]() 在直角坐标系中的普通方程;
在直角坐标系中的普通方程;
(Ⅱ)以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,当曲线
轴的正半轴为极轴建立极坐标系,当曲线![]() 截直线
截直线![]() 所得线段的中点极坐标为
所得线段的中点极坐标为![]() 时,求直线
时,求直线![]() 的倾斜角.
的倾斜角.
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的焦点是
的焦点是![]() ,
,![]() ,且过点
,且过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过左焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,
两点,![]() 为坐标原点.问椭圆
为坐标原点.问椭圆![]() 上是否存在点
上是否存在点![]() ,使线段
,使线段![]() 和线段
和线段![]() 相互平分?若存在,求出点
相互平分?若存在,求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第二届中国国际进口博览会于2019年11月5日至10日在上海国家会展中心举行.它是中国政府坚定支持贸易自由化和经济全球化,主动向世界开放市场的重要举措,有利于促进世界各国加强经贸交流合作,促进全球贸易和世界经济增长,推动开放世界经济发展.某机构为了解人们对“进博会”的关注度是否与性别有关,随机抽取了100名不同性别的人员(男、女各50名)进行问卷调查,并得到如下![]() 列联表:
列联表:
男性 | 女性 | 合计 | |
关注度极高 | 35 | 14 | 49 |
关注度一般 | 15 | 36 | 51 |
合计 | 50 | 50 | 100 |
(1)根据列联表,能否有99.9%的把握认为对“进博会”的关注度与性别有关;
(2)若从关注度极高的被调查者中按男女分层抽样的方法抽取7人了解他们从事的职业情况,再从7人中任意选取2人谈谈关注“进博会”的原因,求这2人中至少有一名女性的概率.
附:![]() .
.
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆C上.
在椭圆C上.
(1)求椭圆C的标准方程;
(2)若直线上![]() 与C交于A,B两点,是否存在l,使得点
与C交于A,B两点,是否存在l,使得点![]() 在以AB为直径的圆外.若存在,求出k的取值范围;若不存在,请说明理由.
在以AB为直径的圆外.若存在,求出k的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧棱
中,侧棱![]() 平面
平面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]()
![]() ,
,![]() ,
,![]() ,
,![]() .
.
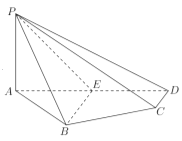
(1)求二面角![]() 的余弦值;
的余弦值;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出点
?若存在,求出点![]() 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com