
【题目】已知方程x2+y2﹣2x﹣4y+m=0.
(1)若此方程表示圆,求m的取值范围;
(2)若(1)中的圆与直线x+2y﹣4=0相交于M、N两点,且OM⊥ON(O为坐标原点),求m;
(3)在(2)的条件下,求以MN为直径的圆的方程.
【答案】
(1)解:(x﹣1)2+(y﹣2)2=5﹣m,∴方程表示圆时,m<5
(2)解:设M(x1,y1),N(x2,y2),则x1=4﹣2y1,x2=4﹣2y2,得x1x2=16﹣8(y1+y2)+4y1y2,
∵OM⊥ON,∴x1x2+y1y2=0,∴16﹣8(y1+y2)+5y1y2=0①,
由 ![]() ,得5y2﹣16y+m+8=0,
,得5y2﹣16y+m+8=0,
∴ ![]() ,
, ![]() .
.
代入①得 ![]() .
.
(3)解:以MN为直径的圆的方程为(x﹣x1)(x﹣x2)+(y﹣y1)(y﹣y2)=0,
即x2+y2﹣(x1+x2)x﹣(y1+y2)y=0,
∴所求圆的方程为 ![]()
【解析】(1)圆的方程化为标准方程,利用半径大于0,可得m的取值范围;(2)直线方程与圆方程联立,利用韦达定理及OM⊥ON,建立方程,可求m的值;(3)写出以MN为直径的圆的方程,代入条件可得结论.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知等比数列{an}中,a2=2,a5=128.
(1)求通项an;
(2)若bn=log2an , 数列{bn}的前n项和为Sn , 且Sn=360,求n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
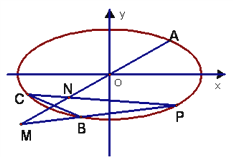
【题目】如图,在平面直角坐标系中,已知A、B、C是椭圆![]() 上不同的三点,
上不同的三点,  ,C在第三象限,线段BC的中点在直线OA上。
,C在第三象限,线段BC的中点在直线OA上。
(1)求椭圆的标准方程;
(2)求点C的坐标;
(3)设动点P在椭圆上(异于点A、B、C)且直线PB, PC分别交直线OA于M、N两点,证明![]() 为定值并求出该定值.
为定值并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 支篮球队进行单循环比赛(任两支球队恰进行一场比赛),任两支球队之间胜率都是
支篮球队进行单循环比赛(任两支球队恰进行一场比赛),任两支球队之间胜率都是![]() .单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.有下列四个命题:
.单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.有下列四个命题:
![]() :恰有四支球队并列第一名为不可能事件;
:恰有四支球队并列第一名为不可能事件; ![]() :有可能出现恰有两支球队并列第一名;
:有可能出现恰有两支球队并列第一名;
![]() :每支球队都既有胜又有败的概率为
:每支球队都既有胜又有败的概率为![]() ;
; ![]() :五支球队成绩并列第一名的概率为
:五支球队成绩并列第一名的概率为![]() .
.
其中真命题是
A. ![]() ,
,![]() ,
,![]() B.
B. ![]() ,
,![]() ,
,![]() C.
C. ![]() .
.![]() .
.![]() D.
D. ![]() .
.![]() .
.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】回答下列问题
(1)已知圆C的方程为x2+y2=4,直线l过点P(1,2),且与圆C交于A、B两点.若|AB|=2 ![]() ,求直线l的方程;
,求直线l的方程;
(2)设直线l的方程为(a+1)x+y﹣2﹣a=0(a∈R).若直线l在两坐标轴上的截距相等,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)= ![]() sin(2x﹣
sin(2x﹣ ![]() )+1的图象向左平移
)+1的图象向左平移 ![]() 个单位长度,再向下平移1个单位长度后,得到函数g(x)的图象,则函数g(x)具有的性质(填入所有正确的序号) ①最大值为
个单位长度,再向下平移1个单位长度后,得到函数g(x)的图象,则函数g(x)具有的性质(填入所有正确的序号) ①最大值为 ![]() ,图象关于直线x=
,图象关于直线x= ![]() 对称;②在(﹣
对称;②在(﹣ ![]() ,0)上单调递增,且为偶函数;③最小正周期为π;④图象关于点(
,0)上单调递增,且为偶函数;③最小正周期为π;④图象关于点( ![]() ,0)对称,⑤在(0,
,0)对称,⑤在(0, ![]() )上单调递增,且为奇函数.
)上单调递增,且为奇函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知: ![]() 、
、 ![]() 、
、 ![]() 是同一平面上的三个向量,其中
是同一平面上的三个向量,其中 ![]() =(1,2).
=(1,2).
(1)若| ![]() |=2
|=2 ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐标.
的坐标.
(2)若| ![]() |=
|= ![]() ,且
,且 ![]() +2
+2 ![]() 与2
与2 ![]() ﹣
﹣ ![]() 垂直,求
垂直,求 ![]() 与
与 ![]() 的夹角θ
的夹角θ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
已知极坐标系的极点![]() 与直角坐标系的原点重合,极轴与直角坐标系中x轴的正半轴重合.圆C的参数方程为
与直角坐标系的原点重合,极轴与直角坐标系中x轴的正半轴重合.圆C的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ),直线
),直线![]() ,若直线
,若直线![]() 与曲线C相交于A,B两点,且
与曲线C相交于A,B两点,且![]() .
.
(Ⅰ)求![]() ;
;
(Ⅱ)若M,N为曲线C上的两点,且![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com