
|
|


科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 2 |
| x-4 |
| 1 |
| n(m-n) |
查看答案和解析>>
科目:高中数学 来源: 题型:
 附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)
附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)| 5 |
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
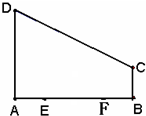 如图直角梯形ABCD中,∠DAB=90°,AD∥BC,E,F是AB边的四等分点,AB=4,BC=BF=AE=1,AD=3,P为在梯形区域内一动点,满足PE+PF=AB,记动点P的轨迹为Γ.
如图直角梯形ABCD中,∠DAB=90°,AD∥BC,E,F是AB边的四等分点,AB=4,BC=BF=AE=1,AD=3,P为在梯形区域内一动点,满足PE+PF=AB,记动点P的轨迹为Γ.查看答案和解析>>
科目:高中数学 来源:2014届湖北省教学合作高三10月联考理科数学试卷(解析版) 题型:选择题
在直角坐标系中,定义两点 之间的“直角距离”为
之间的“直角距离”为 ,
,
现给出四个命题:
①已知 ,则
,则 为定值;
为定值;
②用 表示
表示 两点间的“直线距离”,那么
两点间的“直线距离”,那么 ;
;
③已知 为直线
为直线 上任一点,
上任一点, 为坐标原点,则
为坐标原点,则 的最小值为
的最小值为 ;
;
④已知 三点不共线,则必有
三点不共线,则必有 .
.
A.②③ B.①④ C.①② D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
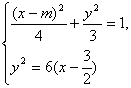 (其中θ为参数)和抛物线
(其中θ为参数)和抛物线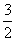 (其中t为参数).
(其中t为参数).(1)是否存在这样的m值,使得该椭圆与该抛物线有四个不同的交点?请说明理由.
(2)当m取何值时,该椭圆与该抛物线的交点与坐标原点的距离等于这个交点与该椭圆中心的距离?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com