
【题目】已知函数f(x)=x2+ax﹣lnx,a∈R.
(1)若a=0时,求函数y=f(x)在点(1,f(1))处的切线方程;
(2)若函数f(x)在[1,2]上是减函数,求实数a的取值范围.
【答案】
(1)解:若a=0时,f(x)=x2﹣lnx的导数为f′(x)=2x﹣ ![]() ,
,
函数y=f(x)在点(1,f(1))处的切线斜率为k=2﹣1=1,切点为(1,1),
则有切线方程为y﹣1=x﹣1,即为x﹣y=0
(2)解:∵函数f(x)在[1,2]内是减函数,
∴f'(x)= ![]() ≤0在[1,2]上恒成立,
≤0在[1,2]上恒成立,
令h(x)=2x2+ax﹣1,有 ![]() 得
得 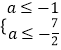 ,
,
∴a≤﹣ ![]()
【解析】(1)求出a=0时函数的导数,求得切线的斜率和切点,由点斜式方程即可得到切线方程;(2)先对函数f(x)进行求导,根据函数f(x)在[1,2]上是减函数可得到其导函数在[1,2]上小于等于0应该恒成立,再结合二次函数的性质可求得a的范围.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两位打字员在两台电脑上各自输入A,B两种类型的文件的部分文字才能使这两类文件成为成品.已知A文件需要甲输入0.5小时,乙输入0.2小时;B文件需要甲输入0.3小时,乙输入0.6小时.在一个工作日中,甲至多只能输入6小时,乙至多只能输入8小时,A文件每份的利润为60元,B文件每份的利润为80元,则甲、乙两位打字员在一个工作日内获得的最大利润是元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市2010年至2016年新开楼盘的平均销售价格y(单位:千元/平米)的统计数据如表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格y | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
(1)求y关于x的线性回归方程;
(2)利用(Ⅰ)中的回归方程,分析2010年至2016年该市新开楼盘平均销售价格的变化情况,并预测该市2018年新开楼盘的平均销售价格.
附:参考数据及公式: ![]() ,
, 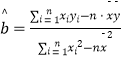 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=1,BC=2,∠CBA= ![]() ,ABEF为直角梯形,BE∥AF,∠BAF=
,ABEF为直角梯形,BE∥AF,∠BAF= ![]() ,BE=2,AF=3,平面ABCD⊥平面ABEF.
,BE=2,AF=3,平面ABCD⊥平面ABEF.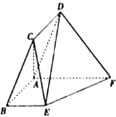
(1)求证:AC⊥平面ABEF;
(2)求平面ABCD与平面DEF所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义 ![]() 为n个正数p1 , p2 , …,pn的“均倒数”.若已知正数数列{an}的前n项的“均倒数”为
为n个正数p1 , p2 , …,pn的“均倒数”.若已知正数数列{an}的前n项的“均倒数”为 ![]() ,又bn=
,又bn= ![]() ,则
,则 ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() =( )
=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ax﹣x3(a>0,且a≠1)恰好有两个不同的零点,则实数a的取值范围是( )
A.1<a<e ![]()
B.1<a<e ![]()
C.0<a<e ![]()
D.e ![]() <a<e
<a<e ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在5件产品中,有3件一等品和2件二等品,从中任取2件,那么以 ![]() 为概率的事件是( )
为概率的事件是( )
A.都不是一等品
B.恰有一件一等品
C.至少有一件一等品
D.至多一件一等品
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是内角A,B,C的对边,且(a+c)2=b2+3ac
(Ⅰ)求角B的大小;
(Ⅱ)若b=2,且sinB+sin(C﹣A)=2sin2A,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex , g(x)=lnx
(1)若曲线h(x)=f(x)+ax2﹣ex(a∈R)在点(1,h(1))处的切线垂直于y轴,求函数h(x)的单调区间;
(2)若函数 ![]() 在区间(0,2)上无极值,求实数a的取值范围.
在区间(0,2)上无极值,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com