
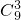 ,
,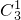 种,再从该类的3个中任取2个共
种,再从该类的3个中任取2个共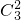 种,
种, 种,故总共
种,故总共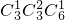 种,
种,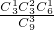 =
=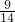 …(4分)
…(4分) =
= ,P(ξ=3)=
,P(ξ=3)=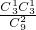 =
= ,
,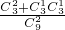 =
= ,P(ξ=5)=
,P(ξ=5)=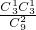 =
= ,P(ξ=6)=
,P(ξ=6)= =
= ,
,| ξ | 2 | 3 | 4 | 5 | 6 |
| P |  |  |  |  |  |
 =4 …(10分)
=4 …(10分) …(12分)
…(12分)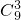 ,事件A,可从三类中任取一类,再从该类的3个中任取2个,然后再从其余两类的6个中任取1个,由分步计数原理可得种数,进而可得概率;(Ⅱ)①ξ可能的取值为2,3,4,5,6,分别求其概率可得分布列;②易求得期望E(ξ),进而可得E(η),由E(η)>1可得关于λ的不等式,解之可得.
,事件A,可从三类中任取一类,再从该类的3个中任取2个,然后再从其余两类的6个中任取1个,由分步计数原理可得种数,进而可得概率;(Ⅱ)①ξ可能的取值为2,3,4,5,6,分别求其概率可得分布列;②易求得期望E(ξ),进而可得E(η),由E(η)>1可得关于λ的不等式,解之可得.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:青岛一模 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2013年山东省青岛市高考数学一模试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com