
分析 (Ⅰ)过切点P(3,2)且与x+y-1=0垂直的直线为y=x-5,与直线y=-4x联立,解得圆心为(1,-4),由此能求出圆的方程.
(Ⅱ)当斜率不存在时,直线l方程为x=1,满足题意;当斜率存在时,设直线l的方程为 y=k(x-1),由点到直线距离公式结合已知条件推导出不存在这样的实数k.从而所求的直线方程为x=1.
解答 解:(Ⅰ)过切点P(3,2)且与x+y-1=0垂直的直线为y+2=x-3,即y=x-5.(1分)
与直线y=-4x联立,解得x=1,y=-4,
∴圆心为(1,-4),…(2分)
∴半径r=$\sqrt{(3-1)^{2}+(-2+4)^{2}}$=2$\sqrt{2}$,
∴所求圆的方程为(x-1)2+(y+4)2=8.…(4分)
(Ⅱ)①当斜率不存在时,此时直线l方程为x=1,
原点到直线的距离为d=1,
同时令x=1代入圆方程得y=-4$±2\sqrt{2}$,∴|EF|=4$\sqrt{2}$,
∴S△OEF=$\frac{1}{2}×1×4\sqrt{2}=2\sqrt{2}$满足题意,
此时方程为x=1.…(8分)
②当斜率存在时,设直线l的方程为y=k(x-1),
圆心C(1,-4)到直线l的距离d=$\frac{4}{\sqrt{{k}^{2}+1}}$,…(9分)
设EF的中点为D,连接CD,则必有CD⊥EF,
在Rt△CDE中,DE=$\sqrt{8-{d}^{2}}$=$\frac{2\sqrt{2}•\sqrt{{k}^{2}-1}}{\sqrt{{k}^{2}+1}}$,
∴EF=$\frac{4\sqrt{2}•\sqrt{{k}^{2}-1}}{\sqrt{{k}^{2}+1}}$,原点到直线l的距离=$\frac{|k|}{\sqrt{{k}^{2}+1}}$,…(10分)
∴S△OEF=$\frac{1}{2}•$$\frac{4\sqrt{2}•\sqrt{{k}^{2}-1}}{\sqrt{{k}^{2}+1}}$•$\frac{|k|}{\sqrt{{k}^{2}+1}}$=2$\sqrt{2}$,…(12分)
整理,得3k2+1=0,不存在这样的实数k.
综上所述,所求的直线方程为x=1.…(14分)
点评 本题考查圆的方程的求法,考查直线方程存在性的讨论及其求法,具有一定的探索性,对数学思维的要求较高,解题时要注意分类讨论思想的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}+\frac{1}{2}i$ | B. | -$\frac{1}{2}+\frac{1}{2}i$ | C. | -$\frac{1}{2}-\frac{1}{2}i$ | D. | $\frac{1}{2}-\frac{1}{2}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
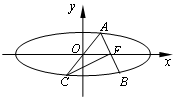 如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点为F,过F的直线交椭圆于A,B两点,点C是点A关于原点O的对称点,若CF⊥AB且CF=AB,则椭圆的离心率为$\sqrt{6}-\sqrt{3}$.
如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点为F,过F的直线交椭圆于A,B两点,点C是点A关于原点O的对称点,若CF⊥AB且CF=AB,则椭圆的离心率为$\sqrt{6}-\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0] | B. | (-∞,1] | C. | (-∞,2] | D. | (-∞,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com