
【题目】已知函数y=acosx+b的最大值为1,最小值为﹣3,试确定 ![]() 的递增区间.
的递增区间.
【答案】解:根据函数y=acosx+b的最大值为1,最小值为﹣3,可得﹣|a|+b=﹣3,|a|+b=1, 解得|a|=2,b=﹣1,
(Ⅰ)当a>0时,a=2,b=﹣1, ![]() ,
,
令2kπ+ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,求得kπ+
,求得kπ+ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,
,
可得函数的增区间为[kπ+ ![]() ,kπ+
,kπ+ ![]() ],k∈Z.
],k∈Z.
(Ⅱ)当a<0时,a=﹣2,b=﹣1,f(x)=﹣sin(﹣2x+ ![]() )=sin(2x﹣
)=sin(2x﹣ ![]() ),
),
令2kπ﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,求得kπ﹣
,求得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,
,
可得函数的增区间为[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z
],k∈Z
【解析】根据三角函数的最值,求得a、b的值,可得f(x)的解析式,再利正弦函数的单调性求得 ![]() 的递增区间.
的递增区间.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】等差数列{an}的前n项和为Sn , 且a3+a5=a4+7,S10=100.
(1)求{an}的通项公式;
(2)求满足不等式Sn<3an﹣2的n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是公差为3的等差数列,数列{bn}满足b1=1,b2= ![]() ,anbn+1+bn+1=nbn . (Ⅰ)求{an}的通项公式;
,anbn+1+bn+1=nbn . (Ⅰ)求{an}的通项公式;
(Ⅱ)求{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边为a,b,c,角A,B,C的大小成等差数列,向量 ![]() =(sin
=(sin ![]() ,cos
,cos ![]() ),=(cos
),=(cos ![]() ,﹣
,﹣ ![]() cos
cos ![]() ),f(A)=
),f(A)= ![]()
![]() ,
,
(1)若f(A)=﹣ ![]() ,试判断三角形ABC的形状;
,试判断三角形ABC的形状;
(2)若b= ![]() ,a=
,a= ![]() ,求边c及S△ABC .
,求边c及S△ABC .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=3sin(2x﹣ ![]() )的图象为C,则下列结论中正确的序号是 . ①图象C关于直线x=
)的图象为C,则下列结论中正确的序号是 . ①图象C关于直线x= ![]() 对称;
对称;
②图象C关于点( ![]() ,0)对称;
,0)对称;
③函数f(x)在区间(﹣ ![]() ,
, ![]() )内不是单调的函数;
)内不是单调的函数;
④由y=3sin2x的图象向右平移 ![]() 个单位长度可以得到图象C.
个单位长度可以得到图象C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆心在y轴上,半径为1,且过点(1,2)的圆的方程为( )
A.x2+(y﹣2)2=1
B.x2+(y+2)2=1
C.(x﹣1)2+(y﹣3)2=1
D.x2+(y﹣3)2=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AC=2 ![]() ,AA1=
,AA1= ![]() ,AB=2,点D在棱B1C1上,且B1C1=4B1D (Ⅰ)求证:BD⊥A1C
,AB=2,点D在棱B1C1上,且B1C1=4B1D (Ⅰ)求证:BD⊥A1C
(Ⅱ)求二面角B﹣A1D﹣C的大小.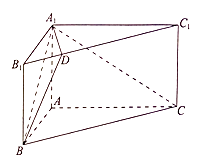
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一房产商竞标得一块扇形OPQ地皮,其圆心角∠POQ= ![]() ,半径为R=200m,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形ABCD的一边AB在半径OP上,C在圆弧上,D在半径OQ;方案二:矩形EFGH的顶点在圆弧上,顶点G,H分别在两条半径上.请你通过计算,为房产商提供决策建议.
,半径为R=200m,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形ABCD的一边AB在半径OP上,C在圆弧上,D在半径OQ;方案二:矩形EFGH的顶点在圆弧上,顶点G,H分别在两条半径上.请你通过计算,为房产商提供决策建议. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com