
【题目】 已知函数![]() .
.
(1)求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)已知函数![]() 区间
区间![]() 上的最小值为1,求实数
上的最小值为1,求实数![]() 的值.
的值.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)求![]() 得切线斜率k,点斜式得方程;(2)法一:
得切线斜率k,点斜式得方程;(2)法一:![]() ,由h(x)单调增,则存在唯一的
,由h(x)单调增,则存在唯一的![]() ,
,![]() ,变形
,变形![]() ,则
,则![]() 构造函数,证明函数有唯一解,即可求解;法一:同法一则
构造函数,证明函数有唯一解,即可求解;法一:同法一则![]() ,利用基本不等式求解即可
,利用基本不等式求解即可
(1)![]()
![]() ,则函数
,则函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ;
;
(2)![]() ,
,![]() ,
,
![]() 在区间
在区间![]() 上单调递增,
上单调递增,![]() 在区间
在区间![]() 上单调递减,存在唯一的
上单调递减,存在唯一的![]() ,
,
使得![]() ,即
,即![]() (*),
(*),
函数![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,![]() 单调递减;
单调递减;![]() ,单调递增,
,单调递增,![]() ,
,
由(*)式得![]() ,
,
![]() ,显然
,显然![]() 是方程的解,
是方程的解,
又![]() 是单调减函数,方程
是单调减函数,方程![]() 有且仅有唯一的解
有且仅有唯一的解![]() ,
,
把![]() 代入(*)式得
代入(*)式得![]() ,
,![]() ,所求实数
,所求实数![]() 的值为
的值为![]() .
.
解法2:![]() ,
,![]() ,
,
![]() 在区间
在区间![]() 上单调递增,
上单调递增,![]() 在区间
在区间![]() 上单调递减,
上单调递减,
所以函数![]() 在
在![]() 上单调递增,故存在唯一的
上单调递增,故存在唯一的![]() ,
,
使得![]() ,即
,即![]() (*),
(*),
![]() ,
,![]() 单调递减;
单调递减;![]() ,单调递增,
,单调递增,![]() ,
,
由![]() 式得
式得![]() ,
,
![]() =
=![]() =
=![]()
![]() ,
,
(当且仅当![]() =1时
=1时![]() ),由
),由![]() 得
得![]() ,此时
,此时![]() ,
,
把![]() 代入(*)也成立,
代入(*)也成立,
∴实数![]() 的值为
的值为![]() .
.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右顶点为
的右顶点为![]() ,上顶点为
,上顶点为![]() .已知椭圆的离心率为
.已知椭圆的离心率为![]() ,
,![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设直线![]() :
:![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,且点
两点,且点![]() 在第二象限.
在第二象限.![]() 与
与![]() 延长线交于点
延长线交于点![]() ,若
,若![]() 的面积是
的面积是![]() 面积的3倍,求
面积的3倍,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
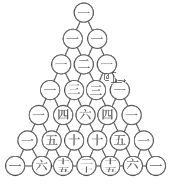
【题目】杨辉三角,又称帕斯卡三角,是二项式系数在三角形中的一种几何排列.在我国南宋数学家杨辉所著的《详解九章算法》(1261年)一书中用如图所示的三角形解释二项式乘方展开式的系数规律.现把杨辉三角中的数从上到下,从左到右依次排列,得数列:1,1,1,1,2,1,1,3,3,1,1,4,6,4,1…….记作数列![]() ,若数列
,若数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中已知A(4,O)、B(0,2)、C(-1,0)、D(0,-2),点E在线段AB(不含端点)上,点F在线段CD上,E、O、F三点共线.
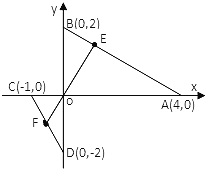
(1)若F为线段CD的中点,证明:![]() ;
;
(2)“若F为线段CD的中点,则![]() ”的逆命题是否成立?说明理由;
”的逆命题是否成立?说明理由;
(3)设![]() ,求
,求![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,且经过点
,且经过点![]() .
.
![]() 求椭圆
求椭圆![]() 的方程;
的方程;
![]() 过点
过点![]() 且不与
且不与![]() 轴重合的直线
轴重合的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,过右焦点
,过右焦点![]() 的直线
的直线![]() 分别交椭圆
分别交椭圆![]() 于点
于点![]() ,设
,设![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是中国古代数学专著,其中的“更相减损术”可以用来求两个数的最大公约数,即“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也,以等数约之.”翻译成现代语言如下:第一步,任意给定两个正整数,判断它们是否都是偶数,若是,用2约简;若不是,执行第二步:第二步,以较大的数减去较小的数,接着把所得的差与较小的数比较,并以大数减小数,继续这个操作,知道所得的数相等为止,则这个数(等数)或这个数与约简的数的乘积就是所求的最大公约数.现给出更相减损术的程序图如图所示,如果输入的![]() ,
,![]() ,则输出的
,则输出的![]() 为( ).
为( ).
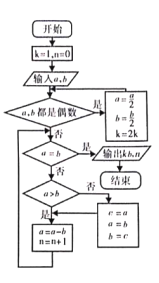
A. 3B. 6C. 7D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com