
【题目】已知函数f(x)=2x-1,![]() (a∈R),若对任意x1∈[1,+∞),总存在x2∈R,使f(x1)=g(x2),则实数a的取值范围是()
(a∈R),若对任意x1∈[1,+∞),总存在x2∈R,使f(x1)=g(x2),则实数a的取值范围是()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
对a分a=0,a<0和a>0讨论,a>0时分两种情况讨论,比较两个函数的值域的关系,即得实数a的取值范围.
当a=0时,函数f(x)=2x-1的值域为[1,+∞),函数![]() 的值域为[0,++∞),满足题意.
的值域为[0,++∞),满足题意.
当a<0时,y=![]() 的值域为(2a,+∞), y=
的值域为(2a,+∞), y=![]() 的值域为[a+2,-a+2],
的值域为[a+2,-a+2],
因为a+2-2a=2-a>0,所以a+2>2a,
所以此时函数g(x)的值域为(2a,+∞),
由题得2a<1,即a<![]() ,即a<0.
,即a<0.
当a>0时,y=![]() 的值域为(2a,+∞),y=
的值域为(2a,+∞),y=![]() 的值域为[-a+2,a+2],
的值域为[-a+2,a+2],
当a≥![]() 时,-a+2≤2a,由题得
时,-a+2≤2a,由题得![]() .
.
当0<a<![]() 时,-a+2>2a,由题得2a<1,所以a<
时,-a+2>2a,由题得2a<1,所以a<![]() .所以0<a<
.所以0<a<![]() .
.
综合得a的范围为a<![]() 或1≤a≤2,
或1≤a≤2,
故选:C.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
【题目】下列命题中,真命题的序号是__________.
①“若![]() ,则
,则![]() ”的否命题;
”的否命题;
②“![]() ,函数
,函数![]() 在定义域内单调递增”的否定;
在定义域内单调递增”的否定;
③“![]() ”是“
”是“![]() ”的必要条件;
”的必要条件;
④函数![]() 与函数
与函数![]() 的图象关于直线
的图象关于直线![]() 对称.
对称.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx![]() x2﹣ax+1.
x2﹣ax+1.
(1)设g(x)=f′(x),求g(x)的单调区间;
(2)若f(x)有两个极值点x1,x2,求证:x1+x2>2.
查看答案和解析>>
科目:高中数学 来源: 题型:
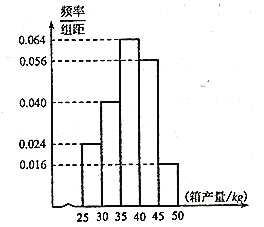
【题目】海水养殖场使用网箱养殖的方法,收获时随机抽取了 100个网箱,测量各箱水产品的产量(单位:![]() ),其频率分布直方图如图:
),其频率分布直方图如图:
定义箱产量在![]() (单位:
(单位:![]() )的网箱为“稳产网箱”, 箱产量在区间
)的网箱为“稳产网箱”, 箱产量在区间![]() 之外的网箱为“非稳产网箱”.
之外的网箱为“非稳产网箱”.
(1)从该养殖场(该养殖场中的网箱数量是巨大的)中随机抽取3个网箱.将频率视为概率,设其中稳产网箱的个数为![]() ,求
,求![]() 的分布列与期望
的分布列与期望![]() ;
;
(2)从样本中随机抽取3个网箱,设其中稳产网箱的个数为![]() ,试比较
,试比较![]() 的期望
的期望![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对一批产品的内径进行抽查,已知被抽查的产品的数量为200,所得内径大小统计如表所示:

(Ⅰ)以频率估计概率,若从所有的这批产品中随机抽取3个,记内径在![]() 的产品个数为X,X的分布列及数学期望
的产品个数为X,X的分布列及数学期望![]() ;
;
(Ⅱ)已知被抽查的产品是由甲、乙两类机器生产,根据如下表所示的相关统计数据,是否有![]() 的把握认为生产产品的机器种类与产品的内径大小具有相关性.
的把握认为生产产品的机器种类与产品的内径大小具有相关性.

参考公式: ,(其中
,(其中![]() 为样本容量).
为样本容量).
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,若已知其在
,若已知其在![]() 内只取到一个最大值和一个最小值,且当
内只取到一个最大值和一个最小值,且当![]() 时函数取得最大值为
时函数取得最大值为![]() ;当
;当![]() ,函数取得最小值为
,函数取得最小值为![]() .
.
(1)求出此函数的解析式;
(2)若将函数![]() 的图像保持横坐标不变纵坐标变为原来的
的图像保持横坐标不变纵坐标变为原来的![]() 得到函数
得到函数![]() ,再将函数
,再将函数![]() 的图像向左平移
的图像向左平移![]() 个单位得到函数
个单位得到函数![]() ,已知函数
,已知函数![]() 的最大值为
的最大值为![]() ,求满足条件的
,求满足条件的![]() 的最小值;
的最小值;
(3)是否存在实数![]() ,满足不等式
,满足不等式![]() ?若存在,求出
?若存在,求出![]() 的范围(或值),若不存在,请说明理由.
的范围(或值),若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 为梯形,
为梯形,![]() ,
,![]() ,且
,且![]() ,
,![]() .
.

(1)求二面角![]() 的大小;
的大小;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com